 |
|
Biography
Robert Kosik was born in Eisenstadt, Austria, in 1969. He studied technical mathematics at the Technische Universität Wien, where he received the degree of diplomingenieur in 1996. In 1998 he joined the Institute for Microelectronics at the Technische Universität Wien and received his PhD degree in 2004. His scientific interests include partial differential equations for transport modeling and data analysis in reliability.
A Revised Wigner Function Approach for Stationary Quantum Transport
Quantum electron transport in modern semiconductor devices is described by a Wigner equation formally similar to the classical Liouville equation (also called the Vlasov equation). The Wigner equation describing stationary quantum transport has a singularity at the point k = 0. Deterministic solution methods usually deal with the singularity by just avoiding that point in the mesh (e.g. Frensley's method). Results from these methods are known to depend strongly on the discretization and meshing parameters. The method is not stable under mesh refinement, and results can even be unphysical.
We propose a revised approach that explicitly includes the point k = 0 in the mesh. For this, we provide two equations for k = 0. The first condition is an algebraic constraint that ensures that the solution of the Wigner equation has no singularity for k = 0. If this condition is fulfilled, we can then derive a transport equation for k = 0 as a secondary equation. The resulting system with two equations for k = 0 is overdetermined, and we call it the constrained Wigner equation.
A theoretical analysis of the overdeterminacy is given by relating the two equations for k = 0 to boundary conditions for the sigma equation, which is the inverse Fourier transform of the Wigner equation. The algebraic constraint is related to periodic boundary conditions, while the transport equation is related to anti-periodic boundary conditions. Together, this is equivalent to double homogeneous boundary conditions in s-space. The constrained sigma equation is the sigma equation with double homogeneous boundary conditions plus inflow boundary conditions via the Fourier transform.
For a test of the revised approach, we simulate Tsuchiya's resonant tunneling device. The constrained sigma equation is solved using a least squares approach where the constraints are fulfilled exactly. The coherence length used in the simulation is 36 nm. The simulation is done for two grid sizes. The dotted line depicts the results for (Nr = 500, Ns = 400). The grid is then refined once in each dimension. The dashed line shows the results for (Nr = 1000, Ns = 800). As seen in Fig. 1, the solution of the constrained sigma equation changes with refinement, but it is quite stable. No numerical parameter fitting is needed.
In the same figure, the two constrained solutions are compared with results from the quantum transmitting boundary method (QTBM). The fit with the QTBM (solid line) is reasonably good for the resonance peak. At a higher bias, we get a discrepancy that requires further research. We believe that the initial results for the constrained equation, as demonstrated in Fig. 1, are encouraging and that the revised method deserves further in-depth study.
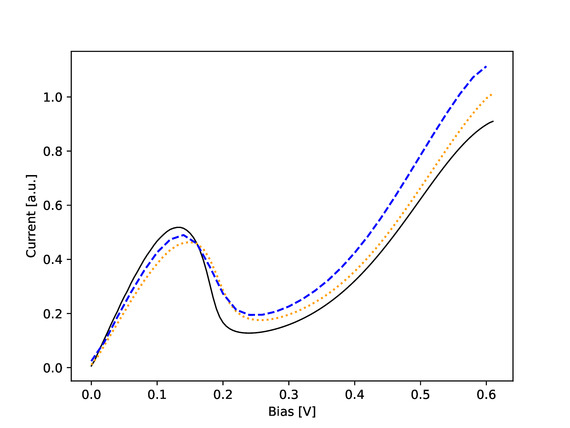
Fig. 1: Solution of the constrained equation. The resonance from the QTBM is reproduced. No parameter fitting is required. The method is stable under mesh refinement.



