 |
|
Biography
D.Sc. Dr. Mihail Nedjalkov, born in Sofia, Bulgaria received the Master degree in semiconductor physics at the Sofia University "Kl. Ohridski", a Ph.D. (Dr.) degree in Physics (1990), Habilitation (2001) and Doctor of Science (D.Sc.) degree in Mathematics (2011) at the Bulgarian Academy of Sciences (BAS). He is Associate Professor with the Institute of Information and Communication Technologies, BAS. He held visiting research positions at the University of Modena (1994), University of Frankfurt (1998), Arizona State University (2004) and mainly at the Institute for Microelectronics, TU-Vienna, supported by the following European and Austrian projects: EC Project NANOTCAD (2000-03),"Österreichische Forschungsgemeinschaft MOEL 239 and 173 (2007-08), FWF (Austrian Science Fund) P13333-TEC (1998-99), P21685-N22 (2010-2014), P27214-N27(2017- date), START (2005-06), P-21685 (2009-2014), EC-FP7 Project SUPERTHEME and the current H2020 Project SUPERAID7. He has served as a lecturer at the International School of Physics 'Enrico Fermi', Varenna, Italy, and has over 200 publications as a first or second author, among them one book and 35 book contributions. His research interests include physics and modeling of classical and quantum carrier transport in semiconductor materials, devices and nanostructures, collective phenomena, theory and application of stochastic methods.
A Gauge-Invariant Wigner Equation for General Electromagnetic Fields
Wigner quantum mechanics is typically formulated in terms of near electrostatic conditions with a scalar potential gauge used to define the Wigner potential. Theories that aim to generalize this picture for the case of a magnetic field usually involve the choice of a particular gauge in terms of the scalar and vector potentials. The Wigner function is defined via the canonical momentum, obtained from the Weyl map of the gradient of the relative position in a center of mass position representation.
In this approach, the Wigner function and the phase space functions of the generic physical quantities depend on the choice of the gauge. For example, the kinetic momentum is given by the difference between the canonical momentum and the vector potential. In contrast, the expectation value of the kinetic momentum, obtained by averaging this difference with the Wigner function, is a physical observable and hence gauge-invariant. Furthermore, generic physical quantities are usually defined in terms of the kinetic momentum, which makes the latter a variable of choice.
A gauge invariant quantum theory is derived in terms of the kinetic momentum by applying a unitary transform to the density operator. The transform generalizes the Weyl map of the standard Wigner theory and was introduced six decades ago by Stratonovich using an intuitive approach involving the characteristic function of the momentum. Crucially, the equation for the Wigner function depends on the electromagnetic (EM) fields but not on the EM potentials. However, the equation has been derived in a form where the spatial dependence of these fields is replaced by a differential operator. This gives rise to a compact mathematical expression but raises serious computational problems. In particular, the order of the equation with respect to the momentum derivatives varies with the position dependence of the EM fields, hampering any numerical approach.
We derive an alternative form of the equation, which holds for general, inhomogeneous and time-dependent EM conditions and has an explicit mathematical structure with clearly defined differential and integral operations. The equation depends on the EM fields only but in a non-local way. For homogeneous magnetic fields, however, the equation simplifies to a local action of the magnetic forces. As a generic application, we simulate the process of magnetic-field governed tunneling through a single barrier (see Fig. 1). The ViennaWD stochastic simulator based on the signed particle approach has been modified to account for accelerating forces and applied to obtain the simulation data. We conclude that the derived equation presents a computationally feasible task for the important case of homogeneous magnetic fields. The inhomogeneous terms imply the presence of non-local effects.
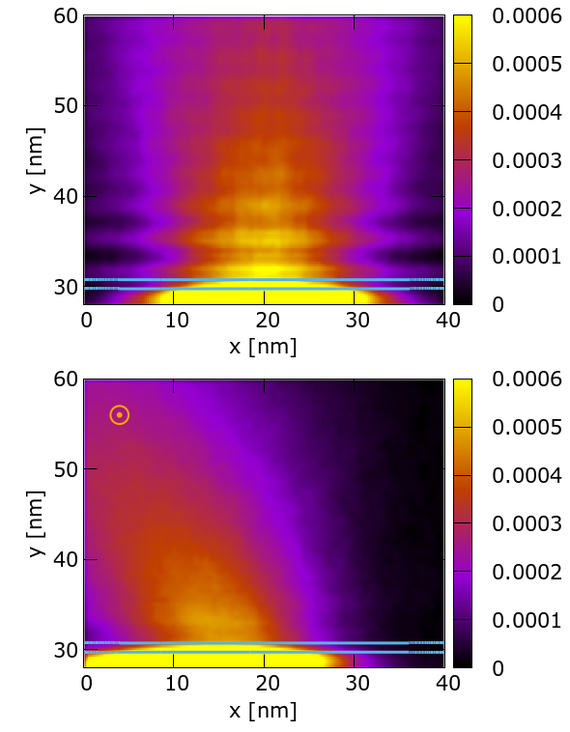
Fig. 1: The density [a.u.] of an electron beam - tunneling trough a barrier marked by the two thin lines (top) - is modified by the B = 6T magnetic field (bottom) by bending the beam and destroying the coherence pattern.



