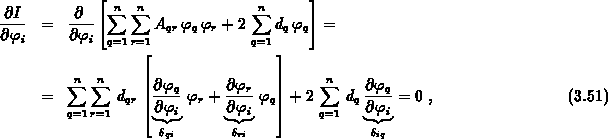3.8 Das Minimum der Variation




Next: 3.8.1 Zweidimensionale Variation
Up: 3 Diskretisierung
Previous: 3.7 Die Elementsmatrizen
Wie schon in Abschnitt 3.3 gezeigt wurde, besitzt
jedes Element mit den lokalen Knotennummern 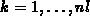 eine fixe Abbildung auf die globalen Gitterknoten.
Jedes Element besitzt einen Abbildungsvektor der Länge
eine fixe Abbildung auf die globalen Gitterknoten.
Jedes Element besitzt einen Abbildungsvektor der Länge 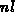 , der einen lokalen
Index
, der einen lokalen
Index 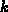 der Elementsmatrix auf einen globalen Index
der Elementsmatrix auf einen globalen Index 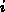 der Gesamtmatrix
der Gesamtmatrix 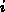 abbildet und
des weiteren als Transformation
abbildet und
des weiteren als Transformation 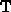 bezeichnet wird.
bezeichnet wird.
Summiert man alle 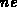 Elementsintegrale zu einem Gesamtintegral
Elementsintegrale zu einem Gesamtintegral

auf, geht man von den lokalen Elementsknoten zu einer globalen Knotennumerierung des
Gesamtgitters mit 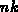 Knoten
Knoten

über und führt man die Dirichletschen Randbedingungen derart ein, daß für die
Dirichlet-Knoten
der Bereich von 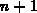 bis
bis 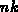 reserviert ist, so erhält man das Gesamtintegral
reserviert ist, so erhält man das Gesamtintegral
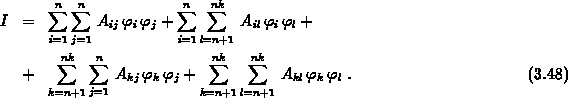
Da die Gesamtmatrix symmetrisch ist, 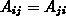 (siehe auch Abschnitt 3.10.1),
vereinfacht sich (3.48) zu
(siehe auch Abschnitt 3.10.1),
vereinfacht sich (3.48) zu
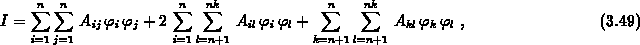
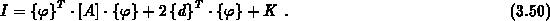
Der letzte Term in (3.49) ist unabhängig von den gesuchten
Potentialen 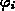 für
für 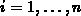 , und wird daher für die weiteren Berechnungen als
Konstante
, und wird daher für die weiteren Berechnungen als
Konstante 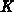 bezeichnet. Die ebenfalls konstante Spaltenmatrix
bezeichnet. Die ebenfalls konstante Spaltenmatrix 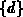 besteht aus
Dirichlet-Knotenwerten, multipliziert mit Matrixkoeffizienten
besteht aus
Dirichlet-Knotenwerten, multipliziert mit Matrixkoeffizienten 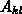 .
.
Bildet man die partiellen Ableitungen nach den unbekannten Knotenpotentialen
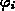 für
für 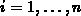 von (3.49) und setzt das Gleichungssystem null,
so hat man das gesuchte Minimum gefunden.
von (3.49) und setzt das Gleichungssystem null,
so hat man das gesuchte Minimum gefunden.
Die partiellen Ableitungen nach der Komponente 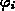 und
und 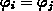 ergeben
ergeben
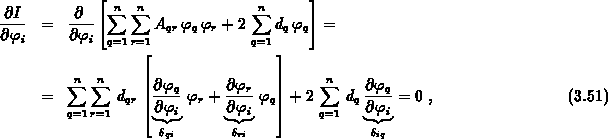
bzw.

Martin Stiftinger
Fri Nov 25 16:50:24 MET 1994
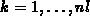 eine fixe Abbildung auf die globalen Gitterknoten.
Jedes Element besitzt einen Abbildungsvektor der Länge
eine fixe Abbildung auf die globalen Gitterknoten.
Jedes Element besitzt einen Abbildungsvektor der Länge 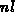 , der einen lokalen
Index
, der einen lokalen
Index 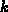 der Elementsmatrix auf einen globalen Index
der Elementsmatrix auf einen globalen Index 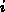 der Gesamtmatrix
der Gesamtmatrix 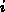 abbildet und
des weiteren als Transformation
abbildet und
des weiteren als Transformation 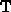 bezeichnet wird.
bezeichnet wird.




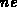 Elementsintegrale zu einem Gesamtintegral
Elementsintegrale zu einem Gesamtintegral

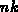 Knoten
Knoten

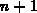 bis
bis 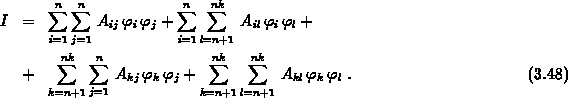
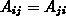 (siehe auch Abschnitt
(siehe auch Abschnitt 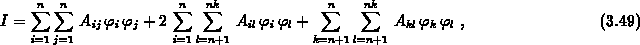
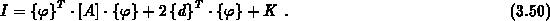
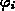 für
für 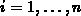 , und wird daher für die weiteren Berechnungen als
Konstante
, und wird daher für die weiteren Berechnungen als
Konstante 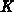 bezeichnet. Die ebenfalls konstante Spaltenmatrix
bezeichnet. Die ebenfalls konstante Spaltenmatrix 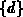 besteht aus
Dirichlet-Knotenwerten, multipliziert mit Matrixkoeffizienten
besteht aus
Dirichlet-Knotenwerten, multipliziert mit Matrixkoeffizienten 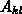 .
.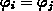 ergeben
ergeben