3.6 Time-dependent SHE of the BTE
First results for a time-dependent SHE using the H-transform have been reported in [75]. However,
the additional derivative,
| ∂tf(x,E,t) | = 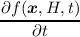 + + 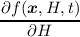 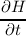 | |
|
| = 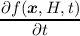 ±∥q∥ ±∥q∥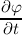 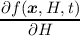 , , | (3.38) |
resulting from the H-transform was not considered in [75] and first reported in [49]. As stated, in a
SHE of the BTE the H-transform is used to eliminate the derivative with respect to energy in the free
streaming operator.
When applying the finite volume method in the energy space, the additional coupling terms
read
| ±∫
Hn-Hn+
∥q∥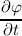 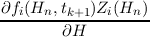 dH dH | |
|
| ⇒±∥q∥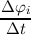 ∫
Hn-Hn+ ∫
Hn-Hn+
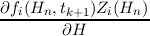 dH dH | |
|
| = ±∥q∥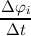 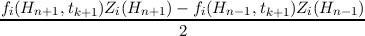 , , | (3.39) |
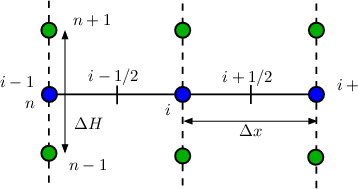
where the subscript i denotes the ith spatial grid point and n is the nth energy grid point (cf. Figure
3.7). The energy space is discretized using equidistant sampling points, that is Hn - Hn-1 = ΔH,
where ΔH is the distance between two adjacent energy grid points. For integration Hn+ and Hn- are
used and defined as
| Hn+ | = (H
n + Hn+1)∕2, | (3.40)
|
| Hn- | = (H
n + Hn-1)∕2. | (3.41) |
Although it is possible to discretize the energy space by non-equidistant grids here, we use
equidistant grids for simplicity. The additional term on the right hand side of Equation
(3.39) couples neighboring energies for even and odd-order unknowns in the system matrix
S
where fe∕o are the even and odd unkowns respectively, be∕o is the right hand side for even and odd
unkowns, See is the upper left sub-matrix coupling even unknowns to even unknowns, and Soo is the
lower right sub-matrix coupling odd-order unknowns with odd-order unknowns, and so forth.
In a SHE of the stationary BTE the sub-matrix Soo is a diagonal matrix. This makes
it possible to reduce the number of unknowns considerably using the Schur-complement
(See -Seo(Soo)-1Soe)xe = be -Seo(Soo)-1bo as shown in [71]. When assembling the time derivative
the coupling of energies introduced by Equation (3.39) for even-order unknowns appearing in See is
similar to any coupling an elastic scattering operator would introduce. But the coupling of the energies
for the odd-order unknowns from Equation (3.39), showing up in Soo, destroys the diagonal
sub-matrix structure of Soo. This in turn increases the effort to eliminate the odd-order unknowns
[71], since one has to carry out multiple line operations to restore the diagonal structure of Soo in
order to reduce the number of unknowns as it is done in a SHE for the time independent BTE
(cf. Figure 3.5).
To account for the time derivative of the expansion coefficients in the expanded BTE, we first
assemble the stationary BTE and include Equation (3.39). Thus, the additional derivative for the total
energy H in Equation (3.38) is accounted for. Now, assuming a known solution fk of the SHE
equations at time tk, the fully assembled SHE equations for the next time tk+1 = tk + Δt without
∂tfn∕p are given as
| Sk+1jf
k+1j = b
k+1j, | | (3.43) |
where j denotes the jth iteration of the non-linear solver (e.g. Newton-Raphson). In order to
assemble the time derivative for tk+1, we use the implicit Euler scheme, although other more
complex higher-order methods are available [76]. After a few algebraic transformations this
yields
Δt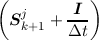 = Δtbk+1j + f
k, = Δtbk+1j + f
k, | | (3.44) |
where I is the unit matrix. Thus, one can assemble the system of SHE-BTE equations in each
iteration of any non-linear solver as before and then include the time derivative by simple algebraic
manipulations of the assembled stationary system of equations.
3.6.1 Comparison to Drift Diffusion
A comparison of the time derivative in the BTE and in the drift diffusion equations can be made by
reproducing and exploring the origins of plasma oscillations. In this section the mathematical
coherences between plasma oscillations as described by the BTE and by the drift diffusion model are
compared.
Oscillations of the whole electron plasma in a semiconductor occur when electrons are shifted out of
their equilibrium position around the fixed ions. Upon relaxation back into their respective
equilibrium positions, the electrons oscillate around their equilibrium position. The characteristic
frequency of plasma oscillations in a semiconductor is
ωp = 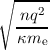 , , | | |
where n is the carrier concentration, me is the electron mass and in this section here κ is used to
denote the dielectric constant. For silicon ωp is usually on the order of 1THz. We expect to see a peak
in the real part of the admittance of a semiconductor device at the plasma frequency [36]. In the
following we will use this fact to asses various assumptions for simulations using SHE and a stability
analysis and show why the plasma frequency is important to test these assumptions. As stated, upon
solving the time-dependent BTE using SHE and the H-transform one has to include an additional
term in the time derivative (cf. Equation (3.38)) due to the H-transform. This term couples
neighboring energies for even and odd-order unknowns. In particular, the coupling of the
energies for the odd-order unknowns destroys the diagonal sub-matrix structure. One possible
way to solve this is to diagonalize the sub-matrix for odd-order unknowns by a suitable
algorithm before applying the algorithm from [71]. Nevertheless, this transformation renders a
required stability analysis intractable. Another possibility to solve this problem is to assume
that the potential change over time (cf. Equation (3.38)) as well as the gradient of the
distribution function over energy are sufficiently small, effectively eliminating the couplings of the
energies for the even and odd-order unknowns. As will be shown, a physically sound way to
solve the problem of additional couplings for odd-order unknowns is to assume that the
time derivative in the equations for the odd-order unknowns is sufficiently small. More
precisely,
Δt-1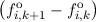 ± ±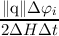 (fi,k+1o(H
n+1) - fi,k+1o(H
n-1)) ≃ 0. (fi,k+1o(H
n+1) - fi,k+1o(H
n-1)) ≃ 0. | | |
In order to assess the physical meaning of the above assumption we take a look at the drift diffusion
model and show that neglecting the time derivative for odd-order unknowns is equivalent to neglecting
the acceleration term
in the drift diffusion model, where J is the current density and τm is the moment relaxation time.
This assumption is equal to neglecting plasma oscillations and was shown to be valid for frequencies
up to the plasma frequency [36]. For the drift diffusion model only the first two moments of the
BTE are used, where closure is obtained by assuming equivalence of carrier temperature
Tn and lattice temperature TL. The moments of the distribution function are calculated
using
⟨ψj⟩ = ∫
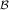 ψjfd3k = w
j ∫ ψjfd3k = w
j ∫
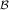 kjfd3k, kjfd3k, | | (3.46) |
where j is the jth moment, ψj denotes the jth weight function and pj is the jth prefactor. To
obtain equations for the moments of the BTE, such as the drift diffusion model, the BTE
is multiplied by increasing integer exponent of the wave vector k and a scalar prefactor
w and afterwards integrated over the Brillouin zone. The first two moments of the BTE
read
| ψ0 | = 1 ⇒⟨ψ0⟩ = ∫
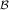 fd3k = n fd3k = n | |
|
| ψ1 | = ℏk ⇒⟨ψ1⟩ = ℏ ∫
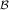 kfd3k kfd3k | |
|
| = ℏ 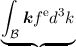 =0 + ∫ =0 + ∫
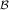 kfod3k kfod3k = J∕q, = J∕q, | | |
where n is the electron density. The integral over the even part cancels out due to the
symmetry of the first Brillouin zone. Thus, the current density is associated with the odd part
or asymmetry of the distribution function. Applying the method of moments, assuming
parabolic bands, and approximating the scattering operator Q{f} using the relaxation time
approximation (RTA), one obtains the drift diffusion model [22]. Repeated from chapter 2
Section 2.3.1, the drift diffusion model with acceleration term, excluding Poisson’s equation,
reads
| ψ0 ⇒ | ∂tn -∥q∥-1∇⋅J
n = -R, | (3.47)
|
| ψ1 ⇒ | τm∂tJn -∥q∥τmkB∇⋅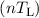 + m*J
n = 0, + m*J
n = 0, | (3.48)
|
| with | ∂tJn = ∫
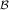 k∂tfd3k = ∂
t ∫ k∂tfd3k = ∂
t ∫
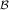 kfod3k kfod3k | (3.49) |
with the mobility μn = ∥q∥τm∕m*, R the scalar recombination term from Rn{fn,fp}, m* is the
effective mass and kB the Boltzmann constant. As derived above the current density is
associated with the odd part of the distribution function and thus also with the odd expansion
orders in a spherical harmonics expansion. Thus neglecting the acceleration term in the DD
model is equivalent to neglecting the time derivative of the odd part of the distribution
function.
3.6.2 Stability
Even if the time derivative has been correctly implemented, numerical stability issues might still araise
and lead to numeric artifacts in the simulation results [77]. At least a guideline, for how small Δx for
spatial, ΔH for energy space and Δt for temporal discretization have to be in order to avoid any
numeric artifacts, is required. To investigate the numerical stability of the time-dependent SHE-BTE a
von Neumann analysis for electrons is carried out. The analysis for holes is done in the same way,
yielding the same results and thus not shown here. Since the full numeric system is too
complex and analytically intractable, we need to simplify matters. Thus, in the following
we neglect plasma oscillations in the calculations to avoid the time derivative of the odd
unknowns in the SHE. To keep the equations in the stability analysis as simple as possible, the
finite volume method (FVM) in the 1D case under bulk conditions for silicon (cf. Figure
3.7) is used. Thus the force F, the generalized density of states Z as well as the group
velocity v(k) are assumed to be spatially constant. To avoid notational clutter we use a
superscript (o) to mark odd-order unknowns, indices and variables. The same is done for
even-order unkowns (superscript e). We also drop the indices l,m, l′,m′ including the
summation over these indices as well as the arguments to the distribution function. Additionally,
we consider only elastic, velocity randomizing scattering processes and neglect the Pauli
principle to further simplify the analysis. To summarize, we condense the scattering operator
to
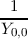 ( (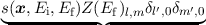 in-scattering - in-scattering -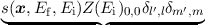 out-scattering) = out-scattering) = 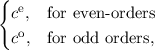 | | |
where Y 0,0 is the first spherical harmonic, s is the scattering rate. Inelastic processes are not
considered in the stability analysis. This assumption is needed to decouple the equations with respect
to the total energy, which in turn leads to a tractable number of equations. Following [66, 47] the
expanded and discretized BTE in a single spatial dimension (cf. Figure 3.7) for odd expansion orders
reads
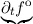 ≃0 ≃0 | + 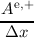 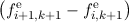 + + 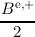 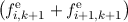 = cof
i+1∕2,k+1o, = cof
i+1∕2,k+1o, | |
|
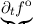 ≃0 ≃0 | + 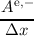 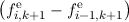 + + 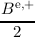 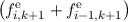 = cof
i-1∕2,k+1o, = cof
i-1∕2,k+1o, | | |
where fi,ke is the even unknown expansion coefficient for l,m at vertex i in the kth time step and fi,ko
is the same for odd unknowns for l′,m′. Note that in the equations above we have neglected the
acceleration term by setting the time derivative for odd unknowns to zero. For even-orders the
expanded BTE in 1D reads
| Δt-1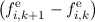 - -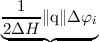 =γ =γ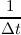 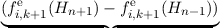 ≃fi,k+1ex ≃fi,k+1ex | |
|
| + 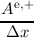 fi+1∕2,k+1o - fi+1∕2,k+1o -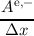 fi-1∕2,k+1o - fi-1∕2,k+1o -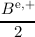 fi-1∕2,k+1o - fi-1∕2,k+1o -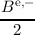 fi+1∕2,k+1o = cef
i,k+1e. fi+1∕2,k+1o = cef
i,k+1e. | | |
Here it was assumed that fi,k+1e(Hn±1) can be written as fi,k+1eχ± and χ = χ+ -χ-, where χ± are
measures of how strong the distribution function increases/decreases over energy. In the above
equations the shorthands
| Ae∕o,± = ∫
Hn-Hn+
jl,ml′,m′(x
i±1∕2,Hn)dH, | | (3.50)
|
| Be∕o,± = ∫
Hn-Hn+
Al,ml′,m′(x
i±1∕2,Hn)dH, | | (3.51) |
have been used for even and odd-orders, where A and j are the shorthands from Equation (3.26) for
integrals over spherical harmonics. In this discretization Ae∕o,± accounts for the projected diffusion
term in the free streaming operator of the BTE, whereas Be∕o,± is the projected drift term and thus
dependent on the driving force (electric field). Since we are assuming a homogeneous material and a
constant driving force, we have Ae,+ = Ae,-, Be,+ = Be,-, Ao,+ = Ao,- and Bo,+ = Bo,-. With the
simplified system given above, a von Neumann stability analysis is possible. For this we
(i) eliminate the odd unknowns in the equation for the even unknowns,
(ii) Fourier transform the obtained equation in space to transform spatial offsets into phase factors
and
(iii) express the gain G as a function of Δx and Δt.
The Fourier transforms, where j is the imaginary unit, of fi,ke and fi,ko read GkFe exp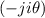 and
GkFo exp
and
GkFo exp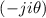 respectively, where G is the gain. Thus one obtains, after a few algebraic
transformations, the gain
respectively, where G is the gain. Thus one obtains, after a few algebraic
transformations, the gain
|G|2 = 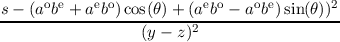 , , | | (3.52) |
where
| s = | cocoΔt-2(aeao + bebo + co(ce - Δt-1 + γχΔt-1) | |
|
| y = | ao2be2 + ae2(ao2 + bo2) | |
|
| + 2aeao(bebo + co(ce - Δt-1 + γχΔt-1)) | |
|
| + (bebo + co(ce - Δt-1 + Δt-1γχ))2, | |
|
| z = | 2(aobe + aebo)(aeao + bebo + co(ce - Δt-1 + γχΔt-1)) | |
|
| cos(θ) + 2aeaobebo cos(θ), | | |
and
ae = 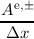 + + 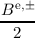 , , | ao = 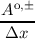 + + 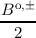 , , | (3.53)
|
be = 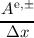 - -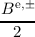 , , | bo = 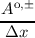 - -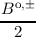 . . | (3.54) |
In order to have numeric stability of the time-discretized SHE-BTE in the von Neumann sense [78],
the following relation must be fulfilled
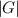 ≤ 1 ⇔ ≤ 1 ⇔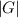 2 ≤ 1, 2 ≤ 1, | | (3.55) |
which states that any frequencies propagated by the BTE must not be amplified. For the lowest
expansion order L = 1 the stability condition reduces to Δt > 0, since for the lowest order we have
c = 0 and B = B′ = 0 due to the H-transform. For L > 1, the stability condition reduces to
provided that
These conditions are naturally fulfilled due to the M-matrix property of the SHE equations for the
lowest expansion order L = 1. In the limit of no driving force,
| Be± = 0and | Bo± = 0andγ = 0, | (3.59) |
or sufficiently small driving force
|Be±|≪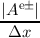 and and | |Bo±|≪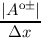 , , | (3.60) |
the stability condition reduces to
Δt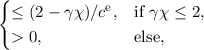 | | (3.61) |
where ce is usually of the order of the density of states. Even though the above relation has been
derived using a number of simplifying assumptions, it can be used as a rough guideline to choose
Δt.
3.6.3 Energy Grid Interpolation
Aside from the usual stability concerns regarding hyperbolic partial differential equations
discretized using the finite volume method, the H-transform poses another restriction to the
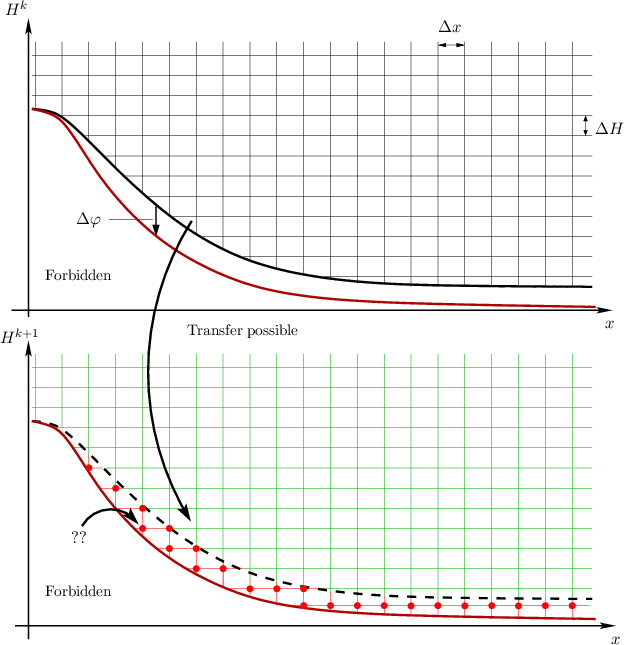
maximum Δt. When considering the time-dependent BTE, the old solution f(x,H,tk) from
time step tk has to be transferred from (x,Hk) to a new grid (x,Hk+1) (cf. Figure 3.6).
Convergence problems and numerical artifacts arise whenever a value of the old distribution
function on (x,Hk) cannot be transferred/interpolated to a point on the new grid (x,Hk+1), because
there is no value of the old distribution function available at that particular energy. This problem is
always present, whenever the potential from time tk to tk+1 = tk + Δt changes by more
than
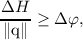 | (3.62) |
where ΔH has to be carefully chosen. One can now either choose ΔH large enough to accommodate a
predicted potential change Δφ within a time step and accept the inaccuracies in the distribution
function introduced by this choice, or choose the boundary conditions for the Poisson equation
and the subsequent time steps carefully in order not to violate Equation (3.62). This is
very unsatisfying, since it is for example not possible to apply step functions as boundary
conditions, with steps larger than Δφ. However, in case one is interested in the small signal
response, a linearization of the free streaming operator of the BTE around the bias point [47]
should be used instead of the time-dependent BTE to avoid the condition in Equation
(3.62).
Even if the condition in Equation (3.62) is not violated, the distribution function f(x,Hk,tk) needs
to be transferred to the new grid such that the macroscopic quantities, that is charge carrier
concentration and charge carrier current, are not modified by the interpolation of f from (x,Hk) to
(x,Hk+1). Thus, the charge carrier density and current density are not modified by the interpolation
of f from (x,Hk) to (x,Hk+1). Since the even part of the distribution function completely defines the
charge carrier concentration and the odd part defines the charge carrier current, the even part is
transferred such that
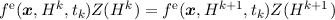 | (3.63) |
holds for the conservation of the carrier density. Likewise the new odd part fo(x,Hk+1,tk+1) is
independently renormalized such that
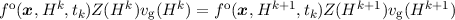 | (3.64) |
is fullfilled, in order to keep the current density constant. However, interpolation errors will occur
during the transfer of the old solution onto the new H-grid, even if the condition in Equation (3.62) is
fulfilled. Since the band edge is shifted by the potential during a single timestep, the first energy grid
point (Hk = 0) closest to the band edge will be shifted under the new band edge or a grid point below
the old band edge (Hk = -1) will be shifted above the new band edge. In the first case a sample
point for the distribution function is lost. In the second case a new energy grid point for
which there is no old distribution function available will be obtained. This effect cannot be
mitigated when the H-transform is employed. The error introduced by this is quantified
by
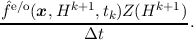 | (3.65) |
3.6.4 Probable Violation of Gauss’ Law
As stated in the previous section, it is currently not possible to avoid errors during energy grid
interpolation. To better understand the implications of this, the discretized SHE-BTE equations per
energy grid point, for a three-point stencil are investigated. In Figure 3.7 a homogeneous, uniformly
discretized three-point stencil for a single spatial dimension is shown. The system of equations for this
simple three point stencil will be derived and evaluated in the following. Assuming that the
even unkowns on the left and right point of this three point stencil are fixed by dirichlet
boundary conditions, only the even expansion coefficient fl,me in the center and the two odd
unkowns on the two edges fl,mo need to be determined. To simplify matters, a first-order
expansion (L = 1) and elastic scattering is assumed. Thus we are left with three unkowns,
the even unkown f0,0i, the odd unknown on the left edge f1,0i-1∕2 and the odd unknown
f1,0i+1∕2 on the right edge. For these unkowns the equations of any point on the H-grid
read
V Zi∂
tf0,0i -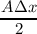 vi-1∕2Zi-1∕2f
1,0i-1∕2 + vi-1∕2Zi-1∕2f
1,0i-1∕2 + 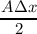 vi+1∕2Zi+1∕2f
1,0i+1∕2 = vi+1∕2Zi+1∕2f
1,0i+1∕2 = | 0, | (3.66)
|
V Zi-1∕2∂
tf1,0i-1∕2 -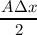 vi-1∕2Zi-1∕2f
0,0i-1 + vi-1∕2Zi-1∕2f
0,0i-1 + 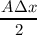 vi-1∕2Zi-1∕2f
0,0i = vi-1∕2Zi-1∕2f
0,0i = | Sf
1,0i-1∕2V, | (3.67)
|
V Zi+1∕2∂
tf1,0i+1∕2 -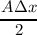 vi+1∕2Zi+1∕2f
0,0i + vi+1∕2Zi+1∕2f
0,0i + 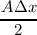 vi+1∕2Zi+1∕2f
0,0i+1 = vi+1∕2Zi+1∕2f
0,0i+1 = | Sf
1,0i+1∕2V, | (3.68) |
where V is the box volume, Z is the generalized density of states, v is the group velocity, S is the
elastic scattering term and the interface area A between two points connected by an edge is
assumed to be equal to unity. Introducing a = (AΔx)∕(2V ), neglecting the time derivatives of
the odd-order unkowns for the sake of argument and using a Backward-Euler scheme one
obtains
| 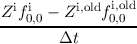 - -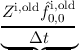 Energy grid interpolation error Energy grid interpolation error | |
|
| + q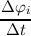 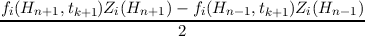 | |
|
| -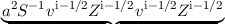 A A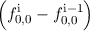 | |
|
| + 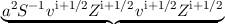 B B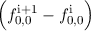 = 0, = 0, | (3.69) |
where the quantities form the previous timestep are highlighted by the superscript old and the energy
grid interpolation error has been considered. Since it will be important when considering the
time derivative, it is shown how to obtain the familiar charge conservation law (Gauss
Law). Integration of the above equation over energy from H = 0 to infinity yields term by
term,
∂tni - (D1 + D2)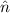 i + 0 + D2ni+1 + 2(D1 + D2)ni - D1ni-1 = 0, i + 0 + D2ni+1 + 2(D1 + D2)ni - D1ni-1 = 0, | | (3.70) |
where D are transport coefficients and
∫
0∞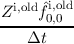 dH dH | = 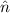 i, i, | (3.71)
|
q ∫
0∞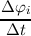 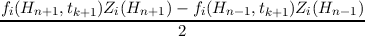 dH dH | = 0. | (3.72) |
If there is no interpolation error at all, i.e. 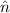 i = 0, one would obtain the familiar charge conversation
law
i = 0, one would obtain the familiar charge conversation
law
| ∂tni - D
1ni-1 + (D
1 + D2)ni - D
2ni+1 = 0, | | (3.73) |
instead. From this it is clear that any energy grid interpolation error leads to artifacts (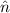 ) in the
charge carrier density.
) in the
charge carrier density.
3.6.5 The Shockley-Haynes Experiment
To assess the derived results we added the time derivative of the BTE to the open source simulator
ViennaSHE [65]. In the first numerical experiment, similar to the famous Shockley-Haynes
experiment in [79], the drift and diffusion of minority carriers in a p-type silicon resistor 5μm long
under carrier-phonon and impurity scattering were investigated. The Shockley-Haynes
experiment was selected, since throughout the whole simulation the potential and thus the
H-grid remain virtually unchanged, provided that the distortion in the carrier concentration
remains small. Assuming symmetry in two axis, the simulation was carried out in a single
dimension using a Δx of 10nm. Additionally, to have the low-field conditions required for
the estimation of the low-field mobility, we chose an uniform electric field of 0.5kV∕cm.
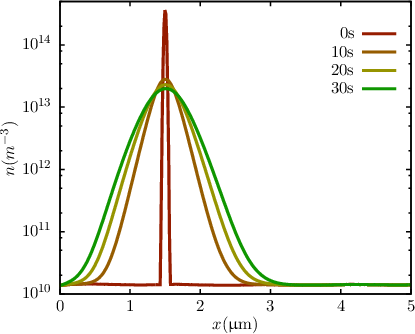
In this initial configuration we artificially introduced, at time zero, a Gaussian disturbance in the
electron density (cf. Figure 3.8), such that changes in the electric field over time can be safely
neglected. This was accomplished by uniformly raising the electron distribution function over the
energy such to reach the desired electron density. Then a time-dependent simulation with a stepping
of Δt = 10ps was carried out. Since changes in the electric field have been kept neglected, the
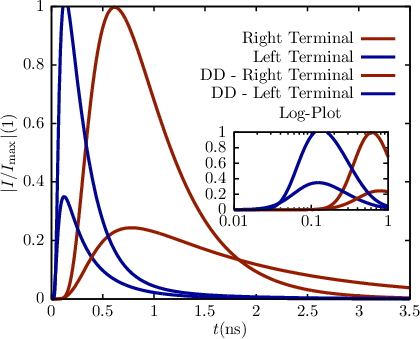
displacement current was neglected too. In the first few hundred picoseconds the high energy carriers
diffuse strongly. Thus, at first most electrons diffuse out of the left terminal before being accelerated
towards the right terminal by the small electric field (cf. Figure 3.9). To see most of the
diffusion in the current, the disturbance has been placed close to the left terminal (cf. Figure
3.10). After 700ps the carrier drift dominates and the current through the right terminal
peaks. One can also calculate the low field mobility from this experiment by observing the
velocity of the electron peak towards the right contact. In the presented experiment we
obtained an electron mobility of 1430cm∕Vs with an uncertainty of ±20cm∕Vs due to the
discretization.
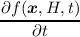 +
+ 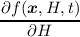
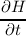
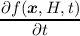 ±∥q∥
±∥q∥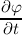
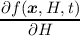 ,
,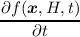 +
+ 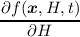
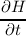
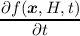 ±∥q∥
±∥q∥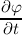
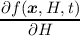 ,
,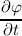
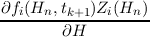 dH
dH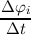 ∫
Hn-Hn+
∫
Hn-Hn+
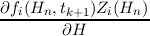 dH
dH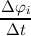
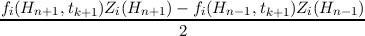 ,
,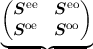 S
S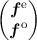 =
= 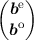 ,
,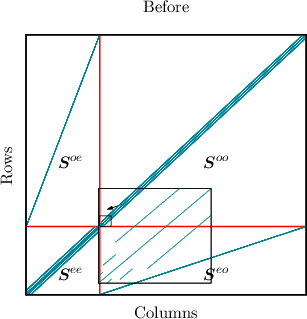
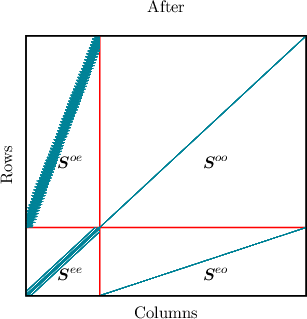
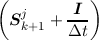 = Δtbk+1j + f
k,
= Δtbk+1j + f
k,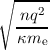 ,
,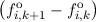 ±
±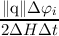 (fi,k+1o(H
n+1) - fi,k+1o(H
n-1)) ≃ 0.
(fi,k+1o(H
n+1) - fi,k+1o(H
n-1)) ≃ 0. ψjfd3k = w
j ∫
ψjfd3k = w
j ∫
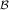 kjfd3k,
kjfd3k,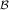 fd3k = n
fd3k = n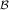 kfd3k
kfd3k
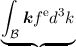 =0 + ∫
=0 + ∫
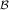 kfod3k
kfod3k = J∕q,
= J∕q,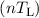 + m*J
n = 0,
+ m*J
n = 0,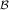 k∂tfd3k = ∂
t ∫
k∂tfd3k = ∂
t ∫
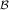 kfod3k
kfod3k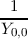 (
(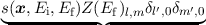 in-scattering -
in-scattering -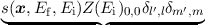 out-scattering) =
out-scattering) = 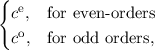
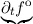 ≃0
≃0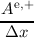
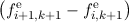 +
+ 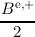
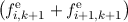 = cof
i+1∕2,k+1o,
= cof
i+1∕2,k+1o,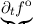 ≃0
≃0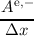
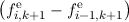 +
+ 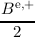
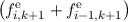 = cof
i-1∕2,k+1o,
= cof
i-1∕2,k+1o,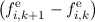 -
-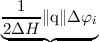 =γ
=γ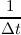
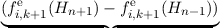 ≃fi,k+1ex
≃fi,k+1ex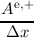 fi+1∕2,k+1o -
fi+1∕2,k+1o -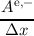 fi-1∕2,k+1o -
fi-1∕2,k+1o -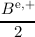 fi-1∕2,k+1o -
fi-1∕2,k+1o -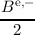 fi+1∕2,k+1o = cef
i,k+1e.
fi+1∕2,k+1o = cef
i,k+1e.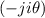 and
GkFo exp
and
GkFo exp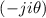 respectively, where G is the gain. Thus one obtains, after a few algebraic
transformations, the gain
respectively, where G is the gain. Thus one obtains, after a few algebraic
transformations, the gain
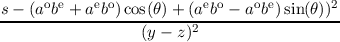 ,
,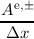 +
+ 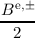 ,
,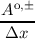 +
+ 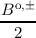 ,
,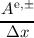 -
-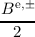 ,
,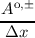 -
-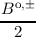 .
.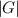 ≤ 1 ⇔
≤ 1 ⇔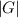 2 ≤ 1,
2 ≤ 1,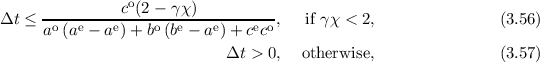
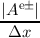 and
and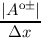 ,
,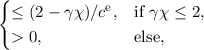
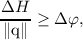
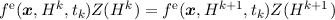
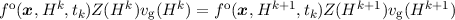
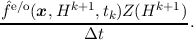
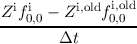 -
-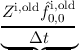 Energy grid interpolation error
Energy grid interpolation error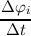
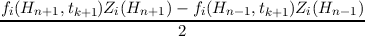
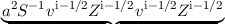 A
A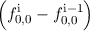
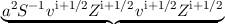 B
B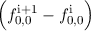 = 0,
= 0,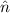 i + 0 + D2ni+1 + 2(D1 + D2)ni - D1ni-1 = 0,
i + 0 + D2ni+1 + 2(D1 + D2)ni - D1ni-1 = 0,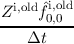 dH
dH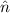 i,
i,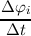
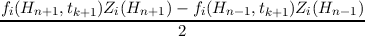 dH
dH i = 0, one would obtain the familiar charge conversation
law
i = 0, one would obtain the familiar charge conversation
law
 ) in the
charge carrier density.
) in the
charge carrier density.