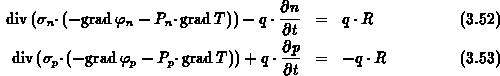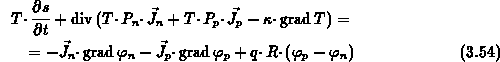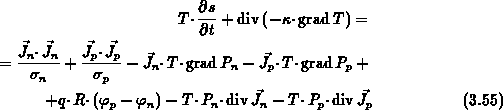3.5 Makroskopische Transportparameter




Next: 3.6 Transformationsbeziehungen von Transportparametern
Up: 3 Ein thermoelektrisches Transportmodell
Previous: 3.4 Phänomenologische Gleichungen
Quasiferminiveaus sind empirisch nicht unmittelbar zugänglich.
Ebenso ist der Energiestrom nicht direkt beobachtbar, wenn sich auch
seine Divergenz als lokale Wärmetönung bemerkbar macht.
Andererseits sind zwei Situationen in der Praxis leicht zu realisieren, der
isothermische Fall und der stromlose Fall.
In diesen Fällen
ist auch eine Messung makroskopischer Transportparameter möglich.
Aus diesen Gründen ist es naheliegend, die phänomenologischen Gleichungen
(3.38), (3.39), (3.40) so umzuformen, daß sie
unter den besagten experimentellen Bedingungen unmittelbar anwendbar sind.
Formal bedeutet dieser Schritt eine Parametrisierung der  mit wenigen unabhängigen Transportparameter, die physikalisch
signifikant und experimentell leicht zugänglich sind, und
außerdem zur
Charakterisierung von Materialeigenschaften verwendet werden können.
Für den thermoelektrischen Transport im Halbleiter werden
die elektrischen Leitfähigkeiten
mit wenigen unabhängigen Transportparameter, die physikalisch
signifikant und experimentell leicht zugänglich sind, und
außerdem zur
Charakterisierung von Materialeigenschaften verwendet werden können.
Für den thermoelektrischen Transport im Halbleiter werden
die elektrischen Leitfähigkeiten 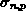 und die
thermoelektrischen Kräfte
und die
thermoelektrischen Kräfte 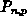 für Elektronen und
Löcher verwendet, sowie die thermische Leitfähigkeit
für Elektronen und
Löcher verwendet, sowie die thermische Leitfähigkeit  .
.
Die Definitionsgleichungen der makroskopischen Transportparameter
geben die experimentelle Situation unmittelbar wieder [35], [91].
Die elektrische Leitfähigkeit 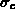 ist die
Ladungsträgerstromdichte pro Einheitsgradienten des
dazugehörigen
Quasifermipotentials unter isothermischen Bedingungen:
ist die
Ladungsträgerstromdichte pro Einheitsgradienten des
dazugehörigen
Quasifermipotentials unter isothermischen Bedingungen:
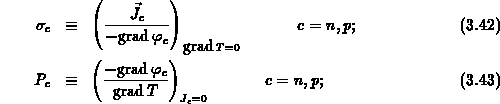
Nach der Definitionsgleichung (3.43) ist die thermoelektrische Kraft
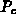 das Verhältnis der Gradienten von Quasifermipotential und
Temperatur.
Gl. (3.43) ist eine Erweiterung der klassischen Definition:
das Verhältnis der Gradienten von Quasifermipotential und
Temperatur.
Gl. (3.43) ist eine Erweiterung der klassischen Definition:
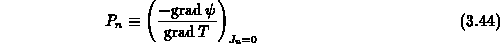
Diese Definition der thermoelektrischen Kraft wurde ursprünglich für
Metalle gegeben, in denen Konzentrationsgradienten keine Rolle spielen.
Sie trifft auch auf den homogenen Halbleiter zu, in dem das chemische
Potential ortsunabhängig ist.
Gl. (3.43) ist insofern eine konsequente Verallgemeinerung von
Gl. (3.44), als alle Effekte, die zur Akkumulation von
Ladungsträgern am kalten Ende beitragen, auch in die Definition der
thermoelektrischen Kraft aufgenommen werden müssen,
unabhängig davon, ob sie experimentell von außen leicht
(wie  ,
,  ) oder schwer (wie
) oder schwer (wie 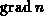 )
beeinflußt werden können.
Die thermoelektrische Kraft (3.43) wird auch als
differentielle oder absolute Thermospannung bezeichnet.
)
beeinflußt werden können.
Die thermoelektrische Kraft (3.43) wird auch als
differentielle oder absolute Thermospannung bezeichnet.
Die Wärmeleitfähigkeit  ist jener Wärmestrom, der pro
Einheit des Temperaturgradienten im stromlosen Fall fließt:
ist jener Wärmestrom, der pro
Einheit des Temperaturgradienten im stromlosen Fall fließt:
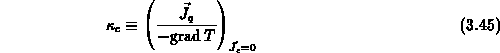
Zur Definition der Wärmeleitfähigkeit (3.45) ist zu
bemerken, daß Stromlosigkeit eigentlich das
Verschwinden der Gesamtstromdichte 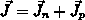 verlangt.
In der Bauelementesimulation wird jedoch der
Elektronen- und Löcherstrom
getrennt beschrieben (siehe Gl. (3.19), (3.20)).
Deshalb ist es angemessen, die Definition der Wärmeleitfähigkeit
bandspezifisch zu geben.
verlangt.
In der Bauelementesimulation wird jedoch der
Elektronen- und Löcherstrom
getrennt beschrieben (siehe Gl. (3.19), (3.20)).
Deshalb ist es angemessen, die Definition der Wärmeleitfähigkeit
bandspezifisch zu geben.
Die Anwendung der Definitionsgleichungen (3.42), (3.43),
(3.45) auf die phänomenologischen Gleichungen der
Form (3.38) liefert folgende Ausdrücke für elektrische
Leitfähigkeiten  ,
thermoelektrische Kräfte
,
thermoelektrische Kräfte 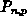 und für die Wärmeleitfähigkeit
und für die Wärmeleitfähigkeit  :
:
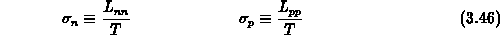
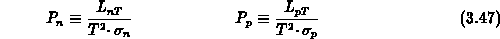
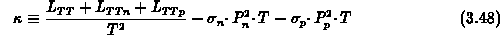
Mit Hilfe von Gl. (3.46), (3.47) und (3.48)
ergeben sich für den thermoelektrischen
Transport im Halbleiter folgende Stromrelationen :
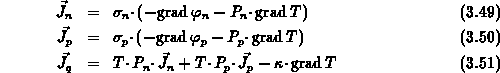
Gl. (3.49), (3.50), (3.51) enthalten beide Grenzfälle,
isothermische elektrische Stromleitung aufgrund angelegter Quasifermipotentiale
und Wärmeleitung im stromlosen Fall, weil ein Temperaturgradient existiert.
Der erste Fall wird durch das Ohmsche Gesetz beschrieben.
Die elektrische Stromdichte in einem isotropen Medium, das auf konstanter
Temperatur gehalten wird, ist mittels einer skalaren, isothermischen
elektrischen Leitfähigkeit 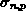 phänomenologisch mit der treibenden Kraft (
phänomenologisch mit der treibenden Kraft (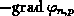 )
verknüpft.
Im Fall stromloser Wärmeleitung (
)
verknüpft.
Im Fall stromloser Wärmeleitung (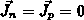 ) reduziert sich
Gl. (3.51)
auf das Gesetz der Wärmeleitung von Fourier.
Es muß nochmals darauf hingewiesen werden, daß die
Wärmeleitfähigkeit (3.48)
den ambipolaren Anteil der Wärmeleitung explizit nicht enthält, weil
) reduziert sich
Gl. (3.51)
auf das Gesetz der Wärmeleitung von Fourier.
Es muß nochmals darauf hingewiesen werden, daß die
Wärmeleitfähigkeit (3.48)
den ambipolaren Anteil der Wärmeleitung explizit nicht enthält, weil
 nach Gl. (3.45) mit der
Nebenbedingung der Stromfreiheit jeweils nur einer Ladungsträgersorte
ermittelt wird.
Die ambipolare Wärmeleitfähigkeit steckt aber
implizit in den Gl. (3.49), (3.50), (3.51).
Sie ergibt sich, wenn Wärmestrom (3.51) und
Wärmeflußgleichung
mit der Gesamtstromdichte
nach Gl. (3.45) mit der
Nebenbedingung der Stromfreiheit jeweils nur einer Ladungsträgersorte
ermittelt wird.
Die ambipolare Wärmeleitfähigkeit steckt aber
implizit in den Gl. (3.49), (3.50), (3.51).
Sie ergibt sich, wenn Wärmestrom (3.51) und
Wärmeflußgleichung
mit der Gesamtstromdichte 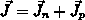 reformuliert werden
(siehe Gl. (4.1), (4.2) im nächsten Kapitel).
Diese Form ist für die Bauelementesimulation jedoch nicht zweckmäßig.
reformuliert werden
(siehe Gl. (4.1), (4.2) im nächsten Kapitel).
Diese Form ist für die Bauelementesimulation jedoch nicht zweckmäßig.
Setzt man die Ladungsträgerstromdichten (3.49),
(3.50) in die Kontinuitätsgleichungen (3.22), (3.23)
ein, erhält man:
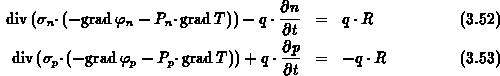
Mit Hilfe des Wärmeflusses (3.51) kann die
Entropiebilanzgleichung (3.36) in eine Wärmeflußgleichung
transformiert werden (3.54):
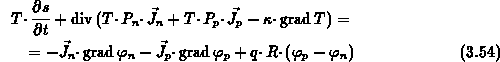
Die Expansion des Divergenzoperators und triviale algebraische Umformungen
ergeben:
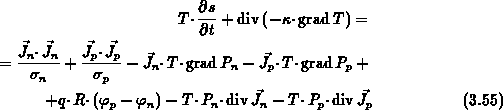
Die rechte Seite von Gleichung (3.55) stellt die Wärmegeneration dar.
Es kann gezeigt werden, daß sie Thomson's Gesetze impliziert
(siehe Gl. (4.2) im nächsten Kapitel).




Next: 3.6 Transformationsbeziehungen von Transportparametern
Up: 3 Ein thermoelektrisches Transportmodell
Previous: 3.4 Phänomenologische Gleichungen
Martin Stiftinger
Sat Jun 10 15:00:12 MET DST 1995
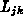 mit wenigen unabhängigen Transportparameter, die physikalisch
signifikant und experimentell leicht zugänglich sind, und
außerdem zur
Charakterisierung von Materialeigenschaften verwendet werden können.
Für den thermoelektrischen Transport im Halbleiter werden
die elektrischen Leitfähigkeiten
mit wenigen unabhängigen Transportparameter, die physikalisch
signifikant und experimentell leicht zugänglich sind, und
außerdem zur
Charakterisierung von Materialeigenschaften verwendet werden können.
Für den thermoelektrischen Transport im Halbleiter werden
die elektrischen Leitfähigkeiten 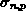 und die
thermoelektrischen Kräfte
und die
thermoelektrischen Kräfte 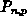 für Elektronen und
Löcher verwendet, sowie die thermische Leitfähigkeit
für Elektronen und
Löcher verwendet, sowie die thermische Leitfähigkeit  .
.




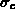 ist die
Ladungsträgerstromdichte pro Einheitsgradienten des
dazugehörigen
Quasifermipotentials unter isothermischen Bedingungen:
ist die
Ladungsträgerstromdichte pro Einheitsgradienten des
dazugehörigen
Quasifermipotentials unter isothermischen Bedingungen:
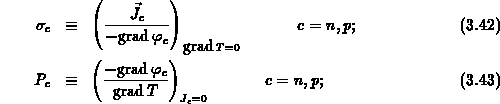
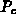 das Verhältnis der Gradienten von Quasifermipotential und
Temperatur.
Gl. (
das Verhältnis der Gradienten von Quasifermipotential und
Temperatur.
Gl. (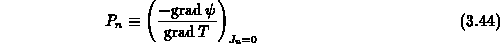
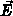 ,
, 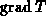 ) oder schwer (wie
) oder schwer (wie 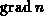 )
beeinflußt werden können.
Die thermoelektrische Kraft (
)
beeinflußt werden können.
Die thermoelektrische Kraft (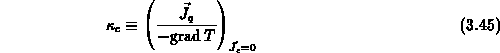
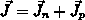 verlangt.
In der Bauelementesimulation wird jedoch der
Elektronen- und Löcherstrom
getrennt beschrieben (siehe Gl. (
verlangt.
In der Bauelementesimulation wird jedoch der
Elektronen- und Löcherstrom
getrennt beschrieben (siehe Gl. (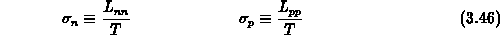
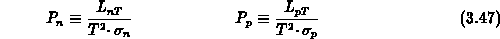
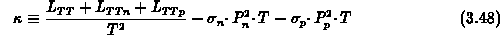
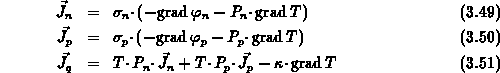
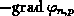 )
verknüpft.
Im Fall stromloser Wärmeleitung (
)
verknüpft.
Im Fall stromloser Wärmeleitung (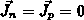 ) reduziert sich
Gl. (
) reduziert sich
Gl. (