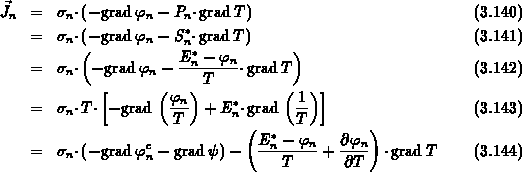
Die Elektronenstromdichte (3.49) kann mit Hilfe von Gl. (3.61) folgendermaßen ausgedrückt werden:
Die resultierende treibende Kraft des Elektronenstroms
kann in Analogie zu Gl. (2.83), (2.84), (2.85), (2.86),
(2.87) verschiedene Formen annehmen.
Makroskopische Transportkoeffizienten sind
in Relation zu bestimmten, einzelnen,
treibenden Kräften derselben resultierenden, treibenden Kraft definiert.
Die Transformation der einzelnen, treibenden Kräfte bedingt eine
Transformation der
Transportkoeffizienten.
Der Vorfaktor des Temperaturgradienten in Gl. (3.142) ist
nach Gl. (3.61) als Transportentropie interpretierbar.
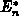stellt die totale innere Energie (Gesamtenergie)
pro Elektroneneinheitsladung dar.
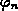enthält das angelegte Potential.
In Gl. (3.144) treten die Gradienten des elektrostatischen Potentials
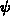, des chemischen Potentials 
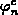und die Temperatur 
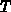als
treibende Kräfte auf.
Die Separation der chemischen von der thermischen Diffusion bedeutet
die Transformation der thermoelektrischen Kraft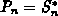 
.
Der Klammerausdruck vor dem Temperaturgradienten in Gl. (3.144)
stellt die kinetische Überschußenergie pro
Elektroneneinheitsladung dar.
Jede der Gl. (3.73), (3.74) bzw. (3.91),
(3.92) kann als eine Bestimmungsgleichung für zwei Unbekannten,
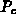und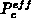 
aufgefaßt werden.
Zur vollständigen Bestimmung von 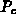, 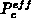ist es ausreichend,
entwe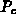der oder 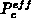zu modellieren.
Wenn es gelingt 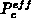zu interpretieren, ergibt
sich die thermoelektrischen Kraft folgerichtig durch Auswertung von
(3.73), (3.74) bzw. (3.91), (3.92).
Die effektive thermoelektrische Kraft beschreibt den Ladungsträgertransport durch Ladungsträgerdiffusion infolge der kinetischen Überschußenergie der Ladungsträger in heißen Gebieten. Mit den Ergebnissen der formalen Transporttheorie (2.98) ergibt sich:
Die effektive thermoelektrische Kraft stellt das Verhältnis der
Thermodiffusivität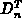 
(Soretkoeffizient) zur Beweglichkeit
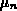dar.
Aufgrund der physikalischen Bedeutung kann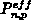 
als Soretfaktor
bezeichnet werden.
In vollkommener Übereinstimmung
mit dem in [188] vorgeschlagenen Modell der Thermodiffusivität
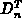folgt aus Gl. (3.145):
Setzt man Gl. (3.146) in Gl. (3.73) ein, ergibt sich der wohlbekannte Ausdruck der thermoelektrischen Kraft der Elektronen im nichtentarteten Halbleiter (z.B. [120], [121], [153], [165], [189]):
Auf analoge Weise erhält man aus Gl. (3.74) die thermoelektrische Kraft der Löcher:
Aus Gl. (3.147),(3.148) ist ersichlich, daß sich die thermoelektrische Kraft aus zwei Beiträgen zusammensetzt. Die ersten beiden Terme in der Klammer stellen die kinetische Transportenergie freier Ladungsträger dar. Der Logarithmus ist nach Gl. (2.57), (2.58) als Fermienergie interpretierbar, die eine potentielle Energie darstellt. Im nicht entarteten Halbleiter addieren sich beide Beiträge, im entarteten Halbleiter bzw. im Metall dagegen subtrahieren sie sich. Deshalb ist die thermoelektrische Kraft im ersten Fall groß, im zweiten Fall klein [192]. Im extrinsischen Halbleiter ist die Fermienergie größer als die kinetische Transportenergie freier Ladungsträger. Die Fermienergie ist als Funktion der Temperatur für n-Leiter negativ [71].
Der Beitrag einer nichtuniformen Temperaturverteilung zum Ladungsträgertransport ist dreifach. Aufgrund der Trägerstatistik ist die Konzentration der Majoritätsträger in Gebieten höherer Temperatur größer, sodaß sich sogar in einem gleichförmig dotierten Halbleiter aufgrund der inhomogenen Temperatur ein Konzentrationsgefälle einstellt, das chemische Diffusion bewirkt. Zudem hängt das Fermipotential von der Temperatur ab, hauptsächlich wegen der Temperaturabhängigkeit der effektiven Zustandsdichte. Der dritte Beitrag ergibt sich aufgrund der unterschiedlichen kinetischen Energie der Ladungsträger, die thermische Diffusion bewirkt.
Der numerische Parameter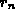 
nimmt für verschiedene dominierende
Streumechanismen unterschiedliche Werte an [121], [153].
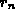kann als Funktion der Beweglichkeiten 
, 
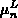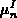berechnet werden [51], sodaß
Gl. (3.146) allgemein folgendermaßen ausgedrückt werden kann:
Gl. (3.150) stellt das Argument von Gl. (3.149) dar.
Der Index 
bezeichnet den Ladungsträgertyp 
oder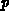 
.
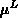ist die Beweglichkeit aufgrund der Gitterstreuung,
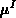aufgrund der Streuung an ionisierten Störstellen.
Im Sonderfall dominierender Gitterstreuung erhält man Stromrelationen wie
in [188].
Einem Hinweis von [170] folgend ist zu Gl. (3.149) anzumerken,
daß der Nenner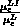 
darstellt [48].
Es sollte gelingen, auch den Zähler in Gl. (3.149) auf verschiedene
Beweglichkeitsbeiträge zurückzuführen, sodaß der
numerische Parameter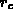 
in kompakterer Form als Funktion
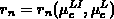ausgedrückt werden kann.
Wenn (3.91), (3.92) als Bestimmungsgleichungen der
thermoelektrischen Kräfte in Silizium aufgefaßt werden, können
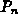und 
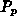mit Hilfe von Gl. (3.149), (3.150) und
(3.130), (3.131), (3.132), (3.136), (3.138)
berechnet werden.
Die Änderung von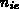 
mit der Temperatur ergibt:
Damit folgt aus Gl. (3.91), (3.92):
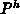ist eine Hilfsgröße:
In den Gl. (3.152), (3.153) bzw. (3.147), (3.148) ist die Abhängigkeit des Fermipotentials von der Gittertemperatur explizit enthalten . Die thermoelektrischen Kräfte (3.152), (3.153) haben im Unterschied zu (3.147), (3.148) die bemerkenswerte Eigenschaft, daß sie wegen (3.154) in hochdotierten Gebieten aufgrund von Hochdotierungseffekten abnehmen. Diese Besonderheit ist als großer Vorteil von (3.152), (3.153) gegenüber (3.147), (3.148) anzusehen. Außerdem wird die Abhängigkeit des Bandabstandes und der effektiven Massen von der Temperatur berücksichtigt.
