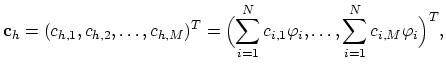


Next: 2.4 Time Dependent Problems
Up: 2. Finite Element Method
Previous: 2.2 Rayleigh-Ritz Method
2.3 Galerkin's Method
A weak formulation of (
 ) for
) for
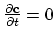 is given by,
is given by,
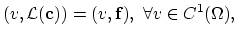 |
(2.7) |
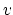 is called test function.
In this case we have an inner product between a scalar and a vector function on both sides of equation (2.7).
is called test function.
In this case we have an inner product between a scalar and a vector function on both sides of equation (2.7).
If the solution of the problem (2.1) in the space
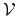 exists, than it is possible to represent this solution as the sum of an infinite series with the weighted basis functions of the space
exists, than it is possible to represent this solution as the sum of an infinite series with the weighted basis functions of the space
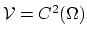 .
.
The central idea of Galerkin's method is to seek the solution of the problem given by (2.1), (2.2), and (2.3) not represented through the basis functions of the infinite space
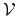 but through the basis functions of the finite space
but through the basis functions of the finite space
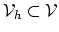 (
dim
(
dim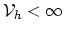 ) [9,10]. Such a solution can only be an approximation of the real solution of (2.1).
) [9,10]. Such a solution can only be an approximation of the real solution of (2.1).
We choose 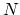 linear independent functions
linear independent functions
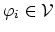 ,
,
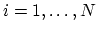 which span the space
which span the space
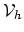 , e.g.
, e.g.
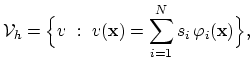 |
(2.8) |
where
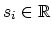 .
.
Now we can write equation (2.7) in the space
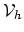 ,
,
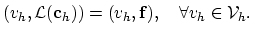 |
(2.9) |
Trivially
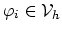 , and we can write,
, and we can write,
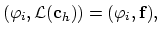 for for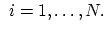 |
(2.10) |
Considering that
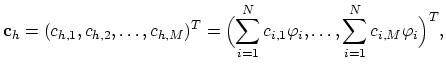 |
(2.11) |
we see that inner product in (2.10) transforms the differential operator
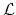 into the operator
into the operator
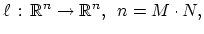 |
(2.12) |
and we write (2.10) as a system of nonlinear algebraic equations
This equation is solved by means of Newton's method (see Section 2.6). The solutions 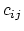 of (2.13) are used to construct approximation of the functions
of (2.13) are used to construct approximation of the functions
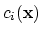 from
from
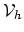 using (2.8).
using (2.8).
The value
is called residuum.



Next: 2.4 Time Dependent Problems
Up: 2. Finite Element Method
Previous: 2.2 Rayleigh-Ritz Method
H. Ceric: Numerical Techniques in Modern TCAD
![]() ) for
) for
![]() is given by,
is given by,
![]() exists, than it is possible to represent this solution as the sum of an infinite series with the weighted basis functions of the space
exists, than it is possible to represent this solution as the sum of an infinite series with the weighted basis functions of the space
![]() .
.
![]() but through the basis functions of the finite space
but through the basis functions of the finite space
![]() (
dim
(
dim![]() ) [9,10]. Such a solution can only be an approximation of the real solution of (2.1).
) [9,10]. Such a solution can only be an approximation of the real solution of (2.1).
![]() linear independent functions
linear independent functions
![]() ,
,
![]() which span the space
which span the space
![]() , e.g.
, e.g.