2.4 Time Dependent Problems

A weak formulation of the problem posed by (2.1), (2.2), and (2.3) is,

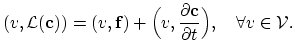$$(v,\mathcal{L}(\mathbf{c}))=(v,\mathbf{f})+\Bigl(v,\frac{\partial \mathbf{c}}{\partial t}\Bigr),\quad \forall v\in \mathcal{V}.$$ (2.15)

Stating the problem in the space 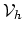$\mathcal{V}_h$, we have,

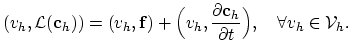$$(v_h,\mathcal{L}(\mathbf{c}_h))=(v_h,\mathbf{f})+\Bigl(v_h,\frac{\partial \mathbf{c}_h}{\partial t}\Bigr),\quad \forall v_h\in \mathcal{V}_h.$$ (2.16)

If we take 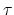$\tau$ as a time step and 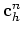$\mathbf{c}_h^n$ as an approximation of 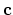$\mathbf{c}$ at the discrete time 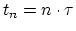$t_n=n\cdot\tau$ in the space 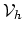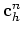$\mathcal{V}_h$, $\mathbf{c}_h^n$ fulfills,

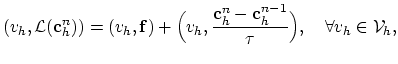$$(v_h,\mathcal{L}(\mathbf{c}_h^n))=(v_h,\mathbf{f})+\Bigl(v_h,\fra... ...athbf{c}_h^n-\mathbf{c}_h^{n-1}}{\tau}\Bigr),\quad \forall v_h\in\mathcal{V}_h,$$ (2.17)

The approach using this representation is known as the backward Euler method. By simple transformation of (2.17) and by introducing the substitution,

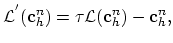$$\mathcal{L}^{'}(\mathbf{c}_h^n)=\tau\mathcal{L}(\mathbf{c}_h^n)-\mathbf{c}_h^n,$$ (2.18)

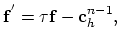$$\mathbf{f}^{'}=\tau\mathbf{f}-\mathbf{c}_h^{n-1},$$ (2.19)

we obtain,

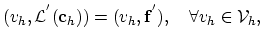$$(v_h,\mathcal{L}^{'}(\mathbf{c}_h))=(v_h,\mathbf{f^{'}}),\quad \forall v_h\in \mathcal{V}_h,$$ (2.20)

which can be treated just like (2.9).