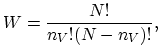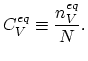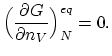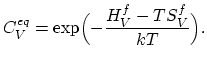


Next: B. Some Tools from
Up: Dissertation Hajdin Ceric
Previous: 5. Summary and Outlook
A perfect crystal at equilibrium at zero temperature is comprised of 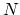 lattice sites, each with a lattice atom.
At any finite temperature, a small population of monovacancies,
lattice sites, each with a lattice atom.
At any finite temperature, a small population of monovacancies, 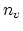 , forms spontaneously, such that the total number of lattice sites increases to
, forms spontaneously, such that the total number of lattice sites increases to
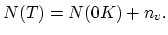 The spontanuos formation of point defect above
The spontanuos formation of point defect above 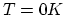 occurs, because the
Gibbs free energy is lowered slightly for a crystal containing a small concentration of vacancies.
A vacancy can be created by removing an atom from its substitional site and placing it on the surface.
The energy required to do this under constant pressure conditions is the entalphy of formation of a vacancy,
occurs, because the
Gibbs free energy is lowered slightly for a crystal containing a small concentration of vacancies.
A vacancy can be created by removing an atom from its substitional site and placing it on the surface.
The energy required to do this under constant pressure conditions is the entalphy of formation of a vacancy, 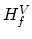 .
According to classical theory for silicon, the formation of vacancy requires the breaking of
four bonds to remove a lattice atom, and the forming of two new bonds
to place this atom on the surface.
New bonds are formed between
dangling bonds of the four neighbors of the vacancy, so that the
neighbors undergo relaxation and distortion.
Then,
.
According to classical theory for silicon, the formation of vacancy requires the breaking of
four bonds to remove a lattice atom, and the forming of two new bonds
to place this atom on the surface.
New bonds are formed between
dangling bonds of the four neighbors of the vacancy, so that the
neighbors undergo relaxation and distortion.
Then,
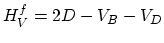 |
(A.1) |
where 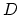 is the bond dissociation energy,
is the bond dissociation energy, 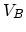 is the energy gained
by bonding between the neighbors of the vacancy, and
is the energy gained
by bonding between the neighbors of the vacancy, and 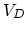 is the
energy associated with deformation of all other bonds.
is the
energy associated with deformation of all other bonds.
The Gibbs free energy of a crystal with 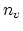 vacancies is,
vacancies is,
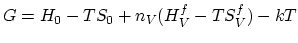 ln ln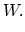 |
(A.2) |
The 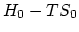 represents the Gibbs free energy of the perfect
vacancy-free crystal and
represents the Gibbs free energy of the perfect
vacancy-free crystal and 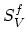 is the disorder induced by
lattice vibration.
The last term on the right side of (A.2) is the
configurational entropy
is the disorder induced by
lattice vibration.
The last term on the right side of (A.2) is the
configurational entropy
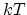 ln
ln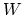 , where
, where
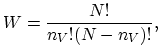 |
(A.3) |
i.e., W is the number of distinguishable ways of distributing 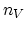 vacancies on
vacancies on 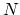 lattice sites.
The equilibrium concentration of lattice vacancies,
lattice sites.
The equilibrium concentration of lattice vacancies,
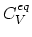 ,
forming at a particular temperature is defined as,
,
forming at a particular temperature is defined as,
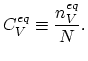 |
(A.4) |
This fractional concentration occurs when the Gibbs free energy
(A.2) is minimized with respect to 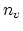 , keeping
, keeping 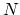 constant,
constant,
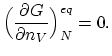 |
(A.5) |
Based on this condition after a few steps of algebra we obtain the
important result,
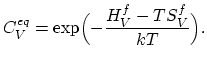 |
(A.6) |
This equation can be generalized to any type of defect.
In semiconductors defects can exhibit various charge states.
For instance in silicon, four charge states have been reported for the
vacancy: 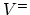 ,
, 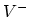 ,
, 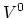 and
and 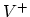 . Under extrinsic
condition, not only does the relative population of the different
charge states change depending on the position of the
electro-chemical potential (Fermi level), but the total concentration
of the point defect in the crystal also changes. It is possible to
directly calculate the concentration of charged defects and express it
in terms of the Fermi level, considering reactions involving the
charged defects which satisfy the charge neutrality constraint.
Let us consider the reaction involving the ionization of the neutral
vacancy
. Under extrinsic
condition, not only does the relative population of the different
charge states change depending on the position of the
electro-chemical potential (Fermi level), but the total concentration
of the point defect in the crystal also changes. It is possible to
directly calculate the concentration of charged defects and express it
in terms of the Fermi level, considering reactions involving the
charged defects which satisfy the charge neutrality constraint.
Let us consider the reaction involving the ionization of the neutral
vacancy 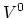 into a positive vacancy,
into a positive vacancy, 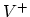 and an electron
and an electron
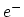 ,
,
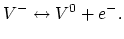 |
(A.7) |
For this reaction, the free energy 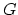 is a minimum at equilibrium
with respect to
is a minimum at equilibrium
with respect to 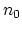 and
and 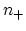 , the number of neutral and
positively charged vacancies, respectively.
This implies that the equilibrium condition
, the number of neutral and
positively charged vacancies, respectively.
This implies that the equilibrium condition 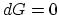 can be written as,
can be written as,
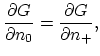 |
(A.8) |
which simply expresses the equality of chemical potentials.
Solving (A.8) allows the relative concentrations of the vacancies to
be written as,
![$\displaystyle \frac{C_{V^{+}}}{C_{V^{0}}}=\frac{Z_{V^{+}}}{Z_{V^{0}}}\exp\Bigl [-\frac{G^{V^{+}}_{F}-G^{V^{0}}_{F}+E_F}{k T}\Bigr],$](img955.png) |
(A.9) |
where,
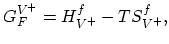 |
(A.10) |
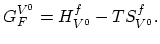 |
(A.11) |
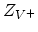 ,
, 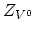 are internal degeneracies and
are internal degeneracies and 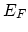 is the Fermi
level. Equation (A.9) is completely general and allows the
concentration of any charged vacancy to be obtained in terms of
is the Fermi
level. Equation (A.9) is completely general and allows the
concentration of any charged vacancy to be obtained in terms of
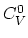 and the Fermi level.
and the Fermi level.



Next: B. Some Tools from
Up: Dissertation Hajdin Ceric
Previous: 5. Summary and Outlook
H. Ceric: Numerical Techniques in Modern TCAD
![]() lattice sites, each with a lattice atom.
At any finite temperature, a small population of monovacancies,
lattice sites, each with a lattice atom.
At any finite temperature, a small population of monovacancies, ![]() , forms spontaneously, such that the total number of lattice sites increases to
, forms spontaneously, such that the total number of lattice sites increases to
![]() The spontanuos formation of point defect above
The spontanuos formation of point defect above ![]() occurs, because the
Gibbs free energy is lowered slightly for a crystal containing a small concentration of vacancies.
A vacancy can be created by removing an atom from its substitional site and placing it on the surface.
The energy required to do this under constant pressure conditions is the entalphy of formation of a vacancy,
occurs, because the
Gibbs free energy is lowered slightly for a crystal containing a small concentration of vacancies.
A vacancy can be created by removing an atom from its substitional site and placing it on the surface.
The energy required to do this under constant pressure conditions is the entalphy of formation of a vacancy, ![]() .
According to classical theory for silicon, the formation of vacancy requires the breaking of
four bonds to remove a lattice atom, and the forming of two new bonds
to place this atom on the surface.
New bonds are formed between
dangling bonds of the four neighbors of the vacancy, so that the
neighbors undergo relaxation and distortion.
Then,
.
According to classical theory for silicon, the formation of vacancy requires the breaking of
four bonds to remove a lattice atom, and the forming of two new bonds
to place this atom on the surface.
New bonds are formed between
dangling bonds of the four neighbors of the vacancy, so that the
neighbors undergo relaxation and distortion.
Then,