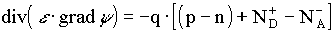 (3/1)
(3/1)
Die Basis aller Berechnungen in einem Halbleiterbauelement bildet die POISSON-Gleichung. Sie kann auf einfache Weise aus den MAXWELLschen Gleichungen abgeleitet werden:
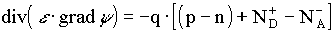 (3/1)
(3/1)
Dabei sind in den Variablen für die Konzentration der ionisierten Dopanden sämtliche Störstellen enthalten. Der Gradient des elektrostatischen Potentials liefert die elektrische Feldstärke:
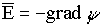 (3/2)
(3/2)
Mit diesen beiden Beziehungen lassen sich nun bei Wahl geeigneter Randbedingungen bereits Potential- und Feldverteilungen in einfachen Halbleitern, bzw. Halbleiterbauelementen - wie z.B. einem MESFET - berechnen. Dies gilt im Prinzip auch für den HFET, jedoch kommt hier erschwerend hinzu, daß eine Bestimmung der quantisierten Energieniveaus in einem Potentialtopf mittels (3/1) und (3/2) nicht möglich ist und damit auch die Information über die zweidimensionale Ladungsträgerkonzentration im Q2DEG fehlt.
Die rechnerische Behandlung eines Q2DEG erfordert eine selbstkonsistente Lösung von POISSON- und SCHRÖDINGER-Gleichung. Die Elektronenwellenfunktionen ergeben sich aus der SCHRÖDINGER-Gleichung in effektiver-Masse-Näherung:
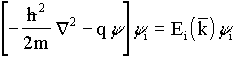 (3/3)
(3/3)
Sofern man vereinfachend nur eine z-Abhängigkeit des Potentials zuläßt, läßt sich diese Gleichung in zwei getrennte SCHRÖDINGER-Gleichungen separieren, wobei die eine als Lösung eine zweidimensionale, quasifreie Bewegung parallel zur Grenzfläche (Heteroübergang) liefert, während für die zweite Lösungen nur für diskrete Energieeigenwerte Ei (Subbänder) existieren, die eine eindimensionale Bewegung senkrecht zur Grenzfläche beschreiben. Die Energieeigenwerte können mit Hilfe der Beziehung (3/4) beschrieben werden:
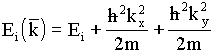 (3/4)
(3/4)
Die numerische Lösung der SCHRÖDINGER-Gleichung erfordert einen erheblichen Aufwand und beansprucht hohe Rechenzeiten. Für spezielle eindimensionale Potentiale existieren Näherungslösungen für die Energieeigenwerte und Wellenfunktionen. Die Lösungen für einen dreiecksförmigen Potentialtopf können wie folgt angegeben werden [37]:
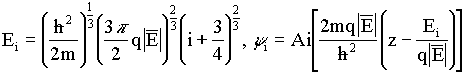 (3/5)
(3/5)
wobei Ai die AIRY-Funktion ist. Für einen rechteckförmigen Potentialtopf findet man [70]:
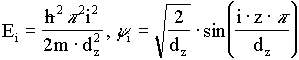 (3/6)
(3/6)
Diese Näherungen sind allerdings nur für unendlich hohe Potentialwände gültig. Im allgemeinen muß die SCHRÖDINGER-Gleichung mit der POISSON-Gleichung selbstkonsistent gelöst werden, wenn man die Quantisierung des Q2DEG in die Berechnung miteinbeziehen will.
Aufgrund des sehr hohen Rechenaufwandes werden SCHRÖDINGER- und POISSON-Gleichung meist nur in eindimensionalen Rechnungen selbstkonsistent gelöst. Ob die Berücksichtigung der SCHRÖDINGER-Gleichung in zweidimensionalen Bauelementsimulatoren den hohen Aufwand an Codierungs- und Rechenzeit rechtfertigt, ist umstritten. Die guten Ergebnisse, die im allgemeinen auch unter Vernachlässigung der Quantisierung in der Simulation zu erzielen sind zeigen, daß die Quantisierung bei Raumtemperatur für viele Bauelementeigenschaften nur einen Effekt höherer Ordnung darstellt. Bei tiefen Temperaturen kommt die Quantisierung dagegen voll zur Geltung.
Innerhalb der vorliegenden Arbeit konnten mit der eindimensionalen selbstkonsistenten Lösung von SCHRÖDINGER- und POISSON-Gleichung interessante Ergebnisse erzielt werden. Die Genauigkeit, mit der dabei Kapazitätscharakteristiken von HFETs reproduziert werden konnten, wird mit dem zweidimensionalen Simulator bisher nicht erreicht. Dies hat letztendlich jedoch nur geringen Einfluß auf die Bestimmung anderer Bauelementeigenschaften, wie z.B. der Transitfrequenz. Ich