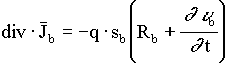3.2 Allgemeine Halbleiter- und
Transportgleichungen

Mit Hilfe der POISSON-Gleichung lassen sich bereits einige statische Eigenschaften eines Halbleiterbauelements charakterisieren. Für die Berechnung des Ladungsträgertransportes muß das Gleichungssystem jedoch mit den Kontinuitätsgleichungen erweitert werden:

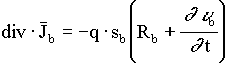(3/7)

Dabei existiert für jede Ladungsträgersorte b eine gesonderte Kontinuitätsgleichung. Die Nettorekombinationsrate eines Ladungsträgertyps Rb beinhaltet alle implementierten Generations- und Rekombinationsmechanismen. Die Stromdichte ist ein Produkt aus Ladungsträgerbeweglichkeit und der "treibenden Kraft":

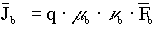(3/8)

Die treibende Kraft enthält neben dem elektrischen Feld auch einen Gradienten der potentiellen Energie (Bandkantenenergie), einen Diffusionsterm, sowie einen Gradienten der Ladungsträgertemperatur. Aus der BOLTZMANN-Gleichung läßt sich für eine hydrodynamische Beschreibung der folgende Ausdruck herleiten:

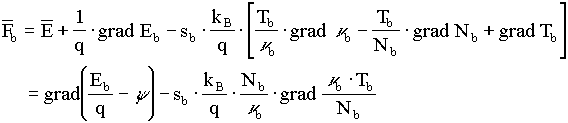(3/9)

Da der Rotor dieses Ausdrucks nicht verschwindet, besitzt dieses Vektorfeld kein Potential. In einer reinen Drift-Diffusionsformulierung kann der treibenden Kraft sehr wohl ein Potential - das Quasi-FERMI-Niveau - zugeordnet werden. In der hydrodynamischen Formulierung gibt es nach dieser Definition im allgemeinen kein Quasi-FERMI-Niveau.

Die in (3/8) vorkommende Ladungsträgerbeweglichkeit ist einer der wichtigsten Transportparameter. In der reinen Drift-Diffusionsformulierung ist die Beweglichkeit eine Funktion der treibenden Kraft, in der hydrodynamischen Formulierung dagegen eine Funktion der Ladungsträgertemperatur. Das in [47] beschriebene Beweglichkeitsmodell wurde im Rahmen dieser Arbeit für verschieden Materialien und Dotierungskonzentrationen angepaßt.

Setzt man in der bisherigen Beschreibung die Ladungsträgertemperatur mit der Gittertemperatur gleich, so entspricht dies bereits einer Drift-Diffusionsbeschreibung. Die in MINIMOS NT implementierte hydrodynamische Beschreibung unterscheidet dagegen zwischen Gitter- und Ladungsträgertemperatur durch die Berücksichtigung des zweiten und dritten Moments der BOLTZMANN-Gleichung in Form der folgenden Energiebilanzgleichung:

(3/10)

Diese Beziehung erhält man über einen Relaxationszeitansatz durch Multiplikation der BOLTZMANN-Gleichung mit ihrem zweiten Moment, der Energiedichte. Entsprechend erhält man durch Multiplikation mit dem nullten, bzw. ersten Moment den Erhaltungssatz für die Teilchenkonzentration und die Teilchenstromdichte.

Die Energiestromdichte - das dritte Moment der BOLTZMANN-Gleichung - setzt sich aus einem konduktiven und einem konvektiven Term zusammen:

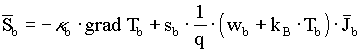(3/11)

Damit ist die Beschreibung des hydrodynamischen Gleichungssystems vollständig. Die Berechnung der verschiedenen Parameter, die in den genannten Gleichungen benötigt werden (wie Ladungsträgerkonzentrationen, Zustandsdichten, Generations-/Rekombinationsraten, etc.), deren Diskretisierung für die verwendete Finite-Boxen Methode, sowie die speziellen Rand- und Übergangsbedingungen werden in [47] beschrieben. Grundlegende Gleichungen können auch der einschlägigen Fachliteratur der Halbleiterphysik (s. z.B. [14, 53, 54, 55, 70, 114]) entnommen werden.