As already mentioned, grain sizes of ferroelectric ceramics can get as small as 10nm. This means that in many cases we do not deal with ideal monocrystals but with structures formed by several grains. The orientations of these grains are not easy to find. As outlined above, the material as a whole shows uniform and, due to the randomly spread orientations, isotropic properties.
Following the ideas outlined in the previous section, the basic
principle of this model is to split the polarization
![]() and the electric field
and the electric field
![]() of the previous operating point
into components in the direction of the next applied electric
field
of the previous operating point
into components in the direction of the next applied electric
field ![]() , resulting in
, resulting in
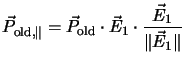 |
(4.18) | ||
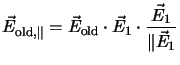 |
(4.19) |
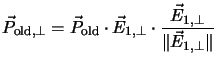 |
(4.20) | ||
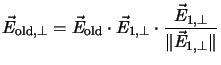 |
(4.21) |
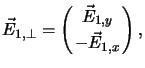 |
(4.22) |
With these geometric operations, the two-dimensional problem gets reduced to two one-dimensional scalar problems, with the additional advantage that this geometric approach also works in three dimensions. Now the concept of Preisach hysteresis, outlined in the previous chapter, can be applied to each of these scalar problems.
For a general approach to two-dimensional hysteresis effects an
inhomogeneous field distribution has to be assumed. This prevents the
usage of a simple one-dimensional hysteresis model which would use an
identical locus curve for the complete ferroelectric region. According
to the algorithm presented above, two different locus curves
![]() and
and
![]() have to be
calculated for each grid point. These are outlined in
Fig. 4.9.
have to be
calculated for each grid point. These are outlined in
Fig. 4.9.
According to the Preisach model, the parameters ![]() and
and ![]() of the
locus curves are calculated using the projections of the old
directions of the old electric field
of the
locus curves are calculated using the projections of the old
directions of the old electric field
![]() ,
,
![]() , the old polarization field
, the old polarization field
![]() ,
,
![]() , and the turning
points
, and the turning
points
![]() ,
,
![]() .
.
The component
![]() in the direction of the electric field
is calculated by entering the signed length of the electric field
vector into the equation of the local locus curve
in the direction of the electric field
is calculated by entering the signed length of the electric field
vector into the equation of the local locus curve
![]()
The actual algorithm required to achieve the signed length
quantity will be discussed in Section 6.2.2. The input for the locus curve is, according to
geometrical properties, zero in the perpendicular direction. Thus with the component
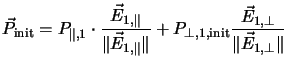 |
(4.25) |
Following the model for the polarization in perpependicular
direction, outlined in Section 4.2.3, the scalar values of the
two components are added and compared to the saturation polarization
![]() .
.
The vanishing electric field in the perpendicular
direction makes it easier to switch the dipoles which are oriented in
this direction than to switch the dipoles which are oriented in the
direction of the electric field and, consequently, hold by it. The
perpendicular component ![]() is reduced appropriately with
respect to the limit
is reduced appropriately with
respect to the limit
| (4.26) |
This is shown schematically in Fig. 4.10
and Fig. 4.11 and leads
to the actual polarization vector
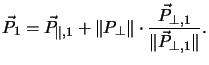 |
(4.27) |