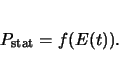5.1 Modeling

For precise simulation a model was developed which allows the analysis of the transient behavior. Simulation in the frequency domain, simulation through simple modification of the hysteresis parameters might be numerically less complex, but will lead to reduced capabilities in comparison with the time domain. Especially in the context of arbitrarily shaped signals and relaxation effects an approach in the time domain is mandatory.

Depending on the concept several different approaches are commonly used. As already outlined in Section 3.2, frequency dependence can be added to compact models by the introduction of additional RC circuits. Other approaches calculate the change of direction of the dipoles with the help of field dependent transition probabilities [TAH+97], or, the speed of domain wall movement, if the focus lies on the analysis of material properties [Ish92][Sco95].

According to the concept of the device simulator MINIMOS-NT, an analytic model based on differential equations was developed. A common approach for the frequency dependence of linear dielectric materials [Fas87] was extended. The approach started out from the static, nonlinear equation

$$P_\mathrm{stat}= f(E(t)).$$ (5.1)

Next a transient term was added to the electric field

$$E(t) = E_\mathrm{stat} + {\tau}_\mathrm{ef} \cdot \frac{dE}{dt},$$ (5.2)

where $E_\mathrm{stat}$ is the static component of the electric field and ${\tau_\mathrm{ef}}$ a material dependent time constant. Then the actual electric field is calculated and entered into (5.1), thus forming the first term for the transient equation

$$P_\mathrm{ef} = f(E(t)).$$ (5.3)

Basically, this term shifts the hysteresis curves and increases the coercive field. Still following the approach for linear materials, a transient term stemming from the change of the polarization

$$P_\mathrm{pol} = - {\tau}_\mathrm{pol}\cdot \frac{dP}{dt}$$ (5.4)

is added. Again ${\tau}_\mathrm{pol}$ is a time constant. In addition to increasing the coercive field, this term also flattens the hysteresis.

Experimental data show that these two terms can be adapted into the physical properties in a limited range of frequencies only. In order to improve this, a third term, which represents the nonlinearity of the material,

$$P_\mathrm{nonlin} = s_h \cdot k_\mathrm{nonlin} \cdot (P - P_\mathrm{ef}) \cdot \frac{dE(t)} {dt},$$ (5.5)

is added, resulting in

$$P = P_\mathrm{ef} + P_\mathrm{pol} + P_\mathrm{nonlin}.$$ (5.6)

$s_h$ is a sign flag indicating whether the electric field is increased or decreased. $k_\mathrm{nonlin}$ is a material dependent coefficient. This term appears to be a good fit and also allows also a physical interpretation as it increases with the distance between the polarization component stemming from the electric field and the actual polarization.