The principles of the KIRKPATRICK point location method can be applied to higher dimensional grids too. The EULER formula as a basis for the proof of the KIRKPATRICK method
(the sum of vertices minus edges plus faces is two, including the unbounded face) can be generalized under the assumption of a simply connected region (i.e. a region with no ``holes'' in it) as
where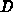 
denotes the (geometric) dimension and 
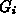the respective geometric
primitive object of dimension 
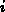(i.e. a point in zero-dimensional space, a
line in one-dimensional space, a triangle in two-dimensional space, a
tetrahedron in three-dimensional space, etc.). The proof for the KIRKPATRICK method can be conducted in the same way, and point location will
still be of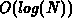 
time. However, it is not clear if the SDAG can be
constructed in 
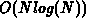time too, as it is the case in two-dimensional
space. Especially techniques for retetrahedralization in linear time in higher
dimensions can not obviously be carried out using similarly structured
algorithms as in two dimensions [Kirk83].
For TCAD applications, the three-dimensional case is of special interest.
Assuming an initial tetrahedral grid, point removal would result in a
star-shaped solid bound by topological two-dimensional geometric primitives
lying in three-dimensional space, i.e. triangles. This star-shaped solid is
now retetrahedralizated, and the new tetrahedrons point to all old intersecting
tetrahedrons. While in two-dimensional space removal of a vertex and
retriangulation will remove a total of two triangles, point removal in three
dimensions results in a total of three removed tetrahedrons. Therefore the
yield is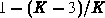 
for a star-shaped solid initially filled by 
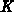tetrahedrons.