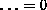Die Gleichungen sind in diskreter Form allgemein so aufgebaut, daß es
zu jeder Variablen des Gleichungssystems eine sogenannte
Kontrollfunktion gibt, das ist jene Funktion, die mit der
auskonvergierten Lösung als Argument Null ergeben muß. Diese
Kontrollfunktion erhält man einfach, indem man die Gleichung in der
Form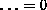 
anschreibt und die linke Seite als Funktion
bezeichnet; die Kontrollfunktion ist also eine implizite Darstellung
der Gleichung.
Solche Kontrollfunktionen zu definieren ist unbedingt notwendig, weil dadurch erst Klarheit über die Vorzeichen der einzelnen Gleichungsbeiträge entstehen kann, die im Simulator an verschiedenen Stellen von durchaus verschiedenen Programmteilen zusammengestellt, weitergeleitet und verschoben werden.
Die Kontrollfunktionen sind nach den Variablen, denen sie zugeordnet
sind, indiziert. Die Variablen sind wieder mit dem Index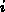 
der
Box/des Gitterpunktes bezeichnet, auf der/dem sie definiert sind.
Pro Variable gibt es eine Gleichung, und daher pro Variable auch eine
Kontrollfunktion.
Eine Kontrollfunktion besteht bei den hier implementierten Gleichungen generell aus zwei verschiedenen Teilen. Der eine Teil bestimmt, welche Beiträge in der Box zu der Kontrollfunktion erbracht werden. In diese Kategorie fallen alle Quellterme, Zeitableitungen, und ähnliche Größen.
Der zweite Teil bestimmt, welche Beiträge durch die Verkopplung der Box mit Nachbarboxen zu der Kontrollfunktion entstehen. Darunter fallen alle Flußterme, wie dielektrischer Fluß, Strom- oder Energiestromfluß, über Ortsdistanzen oder über Materialgrenzen (zum Beispiel Heteroübergänge) hinweg. Dieser zweite Teil ist typischerweise die Diskretisierung eines Differentialoperators des Ortes.
Im Inneren der Segmente stellen die Kontrollfunktionen, die in diesem Kapitel definiert werden, bereits die vollständigen Gleichungen dar. An Rand- und Übergangspunkten dagegen kommen zu diesen Kontrollfunktionen noch weitere Anteile hinzu, die von den Modellen für die spezielle Randsituation stammen. Zusammen ergibt sich eine sogenannte Gesamtkontrollfunktion für die Randbox. In manchen Fällen wird die Kontrollfunktion an Rand- oder Übergangspunkten überhaupt nicht für die entsprechende Gesamtkontrollfunktion benötigt, sondern zu anderen Punkten umgelenkt. Genaueres wird in Kapitel 6 besprochen. Die Gleichungen dieses Kapitels gelten in der angegebenen Form jedenfalls nur an Innenpunkten der Segmente.
Das nichtlineare System von Gleichungen wird in einem iterativen Verfahren gelöst. Während der Iterationen dieses Verfahrens ist die Gleichung einer Variablen nicht gelöst, daher ist die Kontrollfunktion der Variablen nicht Null. Den Wert der Kontrollfunktion bezeichnet man auch als Residuum der entsprechenden Gleichung. An Rand- und Übergangspunkten ist statt der einfachen Kontrollfunktion, die in diesem Kapitel definiert wird, die Gesamtkontrollfunktion für die Ermittlung des Residuums heranzuziehen.