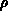Falls die Raumladung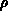 
nicht vom Potential abhängt, die
Poissongleichung also völlig allein steht und mit keiner anderen
Gleichung verkoppelt ist, kann man die Poissongleichung
(3.11) dadurch erfüllen, daß man das lineare Gleichungssystem
löst. Dabei steht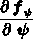 
symbolisch für
die Ableitungsmatrix, gebildet aus den Ableitungen der Komponenten des
Vektors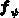 
nach den Komponenten des Vektors 
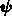und
ausgewertet für das Potential Null. Die rechte Seite ist der
Kontrollfunktionsvektor, ebenfalls ausgewertet für das Potential Null.
Die direkte Lösung des Gleichungssystems ist deshalb möglich, weil
die Funktion 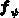linear in 
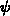ist, was daher kommt,
daß die Ableitungen von (3.12) nach den Werten von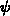
konstant sind.
Man kann also für die Kontrollfunktion den linearisierten Ausdruck
ansetzen, und indem man die Kontrollfunktion Null setzt, erhält man (3.13).
Wenn aufgrund endlicher Abbruchtoleranzen des Gleichungslösers
die Gleichung 3.13 nicht befriedigend gelöst ist, oder wenn
die Raumladung 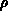eine schwache Abhängigkeit vom Potential
enthält, muß man inkrementell lösen:
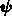Man bestimmt dann aus einer alten Lösung einen
Inkrementvektor (einen update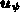 
) gemäß der Gleichung
Dieser Inkrementvektor gibt einen Beitrag an, um den das Potential zu erhöhen ist, damit die Gleichung (3.11) erfüllt ist, wenn die Raumladung gleich bleibt. Ist die Raumladung vom Potential schwach abhängig, so kann (3.11) gelöst werden, indem man (3.15) als Iterationsvorschrift auffaßt und solange wiederholt, bis die Norm des Vektors (3.10) unter eine vordefinierte Fehlertoleranz fällt. Das entspricht dem NEWTON-Verfahren (Kapitel 9) für die alleinstehende Poissongleichung.
