


Next: 7. Examples
Up: 6. Architecture and Implementation
Previous: 6.4.3.2 Cocircular Point Sets
The implemented fully unstructured volume decomposition algorithm is
well suited for remeshing purposes. Mesh points can be erased as well
as inserted, and deformed elements can be discarded.
This full freedom point insertion and removal allows many different kinds of
adaptation techniques. One possibility is the insertion of circumcenters of
not well shaped tetrahedra.
The necessary steps are similar to the described method for inserting
Steiner points at the surface (Section 6.3).
- Find elements which need to be checked for deformations or which
require a mesh update. For example locate the element which contains the
circumcenter of a badly shaped tetrahedron.
- Delete or insert a mesh point by updating the mesh topology and
thereby creating unverified, possibly non-Delaunay tetrahedra.
For example insert the circumcenter as a new mesh point into the found
element.
- Verify the Delaunay criterion for all connected elements and remove
non-Delaunay elements.
- Recurse by removing non-Delaunay elements which are connected
to already removed elements. This is a reversal of the tetrahedra growth
process by the modified advancing front algorithm.
- Reprocessing the combination of the resulting cavity and the mesh
points. No surface preprocessing of the cavity surface is required. The
modified advancing front algorithm performs the tetrahedralization
of the local region by queuing the unconnected triangles. These triangles
must already be Delaunay due to the previous recursive removal process.
All required functions to maintain a consistent data structure have been
implemented for all simplices.
- Create:
- These functions allocate point, triangle, or tetrahedron
entities. The data structure which is composed of a set of consistent
links and references is not yet updated. Only the forward
references will be set. These are the coordinates of a point, the
vertices of a triangle, and a triangle/vertex combination for a
tetrahedron.
- Insert:
- These functions actually insert the created entities by
making the data structure consistent. A consistent data structure is
thereby defined by correct forward and backward
references. For example each point possesses a list of pointers to
incident triangles. A triangle contains pointers to attached tetrahedra.
- Remove:
- These functions are necessary to delete or modify elements.
The element must be cut out leaving a consistent data structure behind.
If a point is removed, all incident triangles and tetrahedra will be
removed to maintain consistency. If a triangle is removed, the
possibly attached tetrahedra will be removed as well.
All backward references have to be updated by setting the
corresponding pointers to removed higher-dimensional elements to null.
This applies only to the maintained data structure and not to the cut out
elements. Thus, through the cut out element all connected and removed
elements are still accessible for e.g. modification purposes. For
example a cut out point may hold references to removed triangles and
tetrahedra.
- Erase:
- These functions finally free the memory space consumed by cut
out elements and their connected higher-dimensional simplices.
- Search:
- Search functions only operate on a consistent data structure
with correct backward references.
- Refine:
- These functions allow the insertion of a point at an arbitrary
position on a given element. Depending on the type of function edges of
triangles, triangles, edges of tetrahedra, triangles of tetrahedra, and
tetrahedra can be refined.
All backward and forward references will be updated
automatically.
Experiments showed that a tetrahedron is ideally represented
by a pointer to a triangle and a pointer to the fourth vertex which closely
reflects the modified advancing front algorithm.
In this way the memory space consumed by a tetrahedron is reduced to two
pointers instead of e.g. four pointers for each vertex.
This type of data structure severely complicated the coding of the
necessary manipulation functions. Especially the refinement functions were
required to evaluate geometric constellations to find a correct combination
of existing oriented triangles and existing points for the creation of new
tetrahedra during the insertion of a refinement point.
Fortunately, only the coding and not the performance during runtime was
affected.
Local transformations were implemented to swap facets and their
attached tetrahedra. With this technique the negative volume (orientation)
sliver elements can be removed.
For the example of such a sliver with a small negative volume the facet
swapping technique modifies the local connectivity between the
neighboring elements in such a way that the sliver element can be
removed and the overlap between two tetrahedra due to the untetrahedralizable
LSPB is resolved.
In this case the resulting topology still fulfills the Delaunay criterion,
because the elements are formed by point sets 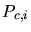 .
.



Next: 7. Examples
Up: 6. Architecture and Implementation
Previous: 6.4.3.2 Cocircular Point Sets
Peter Fleischmann
2000-01-20
![]() .
.