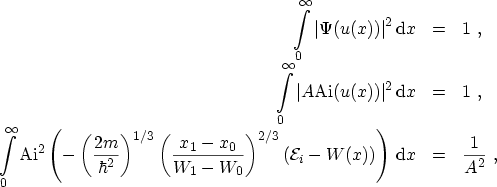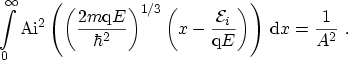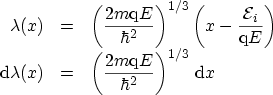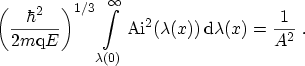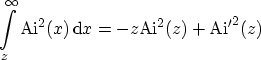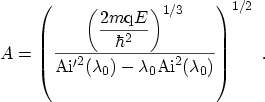C. Wave Function Normalization for a Triangular Potential

For the assumption of a triangular energy well, the wave function is approximately given as (see Section 3.6.1)

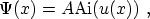$$\Psi(x) = A \ensuremath{\mathrm{Ai}}(u(x)) \ ,$$ (C.1)

with

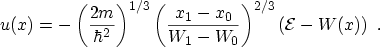$$u(x) = - \left( \frac{2m}{\hbar^2} \right)^{1/3} \left( \frac{x_1 - x_0}{W_1 - W_0} \right)^{2/3} \left({\mathcal{E}}- W(x) \right) \ .$$ (C.2)

The square of the wave function is a probability, therefore the normalization can be written as [156]

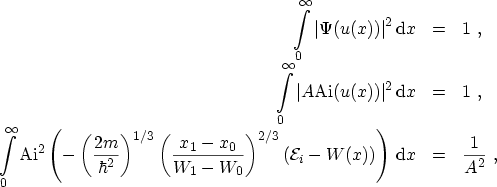$$\begin{array}{rcl} \displaystyle \int_0^\infty \vert\Psi(u(x)... ...h {\mathrm{d}}x &=& \displaystyle \frac{1}{A^2} \ , \end{array}$$ (C.3)

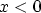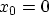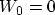where an infinite barrier is assumed for $x<0$. With $x_0 = 0$, $W_0 = 0$, and the electric field

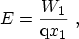$$E = \frac{W_1}{\ensuremath {\mathrm{q}}x_1} \ ,$$ (C.4)

the integral becomes

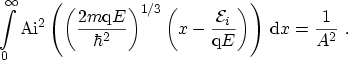$$\int_0^\infty \ensuremath{\mathrm{Ai}}^2 \left( \left( \frac{2m\e... ...h {\mathrm{q}}E}\right) \right) \,\ensuremath {\mathrm{d}}x = \frac{1}{A^2} \ .$$ (C.5)

Substituting

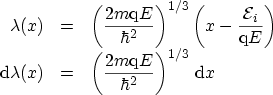$$\begin{array}{rcl} \lambda(x) &=& \displaystyle\left( \frac{2... ...}{\hbar^2} \right)^{1/3}\,\ensuremath {\mathrm{d}}x \end{array}$$ (C.6)

yields

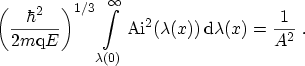$$\left( \frac{\hbar^2}{2m\ensuremath {\mathrm{q}}E} \right)^{1/3} ... ...hrm{Ai}}^2(\lambda(x)) \,\ensuremath {\mathrm{d}}\lambda(x) = \frac{1}{A^2} \ .$$ (C.7)

Using the expression [157]

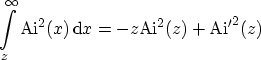$$\int_z^\infty \ensuremath{\mathrm{Ai}}^2(x) \,\ensuremath {\mathrm{d}}x = -z \ensuremath{\mathrm{Ai}}^2(z) + \ensuremath{\mathrm{Ai'}}^2(z)$$ (C.8)

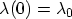and $\lambda(0) = \lambda_0$ the normalization constant becomes

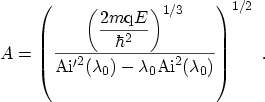$$A = \left( \frac{\left(\displaystyle \frac{2m\ensuremath {\mathrm... ...(\lambda_0) - \lambda_0 \ensuremath{\mathrm{Ai}}^2(\lambda_0)}\right)^{1/2} \ .$$ (C.9)

A. Gehring: Simulation of Tunneling in Semiconductor Devices