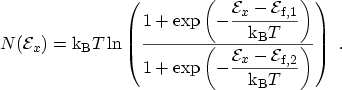In equilibrium the energy distribution function of electrons or holes is given
by the FERMI3.2-DIRAC3.3 statistics
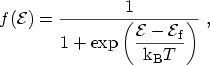 |
(3.15) |
which can be derived from statistical thermodynamics [100].
Separating the longitudinal and transversal energy components
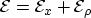 and splitting the integral in (3.14)
and splitting the integral in (3.14)
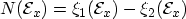 the values of
the values of 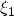 and
and 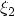 become
become
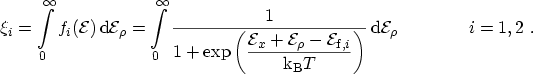 |
(3.16) |
This expression can be integrated analytically using
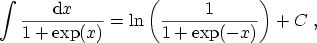 |
(3.17) |
so expression (3.16) evaluates to
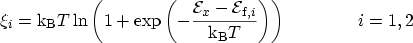 |
(3.18) |
and the total supply function (3.14) becomes
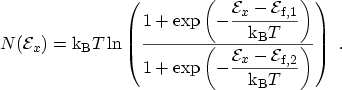 |
(3.19) |
A. Gehring: Simulation of Tunneling in Semiconductor Devices