3.4.1 The Metal-Oxide-Semiconductor Capacitor

Fig. 3.7 shows the band diagram and the electrostatic potential in a metal-oxide-semiconductor structure for different voltages at the metal contact [108,109,110]. A central quantity is the work function which is defined as the energy required to extract an electron from the FERMI energy to the vacuum level. The work function of the semiconductor is

$\displaystyle \ensuremath {\mathrm{q}}\ensuremath {\Phi_\mathrm{S}}= \ensuremat... ...thcal{E}}_\mathrm{v}}+ \ensuremath {\mathrm{q}}\ensuremath {\Phi_\mathrm{f}}\ ,$

(3.43)

where $\chi_s$ denotes the electron affinity of the semiconductor. The work function difference between the work function in the metal $\ensuremath {\mathrm{q}}$ $\ensuremath {\Phi_\mathrm{M}}$ and the work function in the semiconductor $\ensuremath {\mathrm{q}}$ $\ensuremath {\Phi_\mathrm{S}}$ is

$\displaystyle \ensuremath {\mathrm{q}}\ensuremath {\Phi_\mathrm{MS}}= \ensurema... ...ath {\Phi_\mathrm{M}}- \ensuremath {\mathrm{q}}\ensuremath {\Phi_\mathrm{S}}\ .$

(3.44)

The values of $\ensuremath {\Phi_\mathrm{M}}$ and $\ensuremath {\chi_\mathrm{S}}$ depend on the material, as shown in Table 3.1 [100,111,112]. However, the actual value of the work function of a metal deposited on SiO

is not exactly the same as that of the metal in vacuum [112].

As long as BOLTZMANN statistics can be applied, the FERMI potential $\ensuremath {\Phi_\mathrm{f}}$ depends on the doping concentration of the semiconductor in the following way:

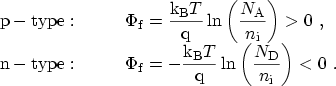$\begin{displaymath}\begin{array}{lcl} \mathrm{p-type:}&\quad &\ensuremath {\Phi_... ...hrm{D}}}{\ensuremath {n_\mathrm{i}}}\right) < 0 \ . \end{array}\end{displaymath}$

(3.45)

The concentration-independent part of (3.44) is labeled $\ensuremath {\Phi_\mathrm{MS}^\prime}$ :

$\displaystyle \ensuremath {\mathrm{q}}\ensuremath {\Phi_\mathrm{MS}^\prime}= \e... ...ensuremath{{\mathcal{E}}_\mathrm{i}}- \ensuremath {{\mathcal{E}}_\mathrm{v}}\ .$

(3.46)

The voltage which has to be applied to achieve flat bands is denoted the flatband voltage. If we deviate from this voltage, a space charge region forms near the interface between the dielectric and the semiconductor. The total potential drop across this space charge region is the surface potential $\ensuremath {\phi_\mathrm{surf}}$ . Due to this potential all energy levels in the conduction and valence bands are shifted by a constant amount, therefore

$\begin{displaymath}\begin{array}{l} \ensuremath {{\mathcal{E}}_\mathrm{c}}(x) = ... ..._{\mathrm{v},0}- \ensuremath {\mathrm{q}}\phi(x)\ , \end{array}\end{displaymath}$

(3.47)

where ${\mathcal{E}}_{\mathrm{c},0}$ and ${\mathcal{E}}_{\mathrm{v},0}$ are the conduction and valence bands in the flatband case. Note that in the flatband case $\phi(x) = 0$ in the whole structure.

**Figure 3.7:** Band diagram and electrostatic potential in an nMOS structure (negative work function difference) in accumulation, under flatband condition, without bias, and under inversion condition.
$\includegraphics[width=.99\linewidth]{figures/mosBarrierBiasHTML}$

Table 3.1: Electron affinity of various semiconductors (left), work function and the radius of the FERMI sphere of various metals (right) [113,114].

Semiconductor	$\ensuremath {\chi_\mathrm{S}}$ [V]	Metal	$\ensuremath {\mathrm{q}}$ $\ensuremath {\Phi_\mathrm{M}}$ [eV]	$\ensuremath {k_\mathrm{f}}\, [\mathrm{nm}^{-1}]$
Si	4.05	Al	4.28	17.52
Ge	4.00	Pt	5.65
GaAs	4.07	W	4.63
GaP	3.80	Mg	3.66	13.74
GaSb	4.06	Ag	4.30	12.04
InAs	4.90	Au	4.80	12.06
InP	4.38	Cu	4.25	13.61
InSb	4.59	Cr	4.50

In metals the FERMI energy is located at a higher energy level than the conduction band. The difference between the conduction band edge in the metal and the FERMI energy in the metal can be calculated considering the free-electron theory of metals which assumes that the metal electrons are unaffected by their metallic ions. The sphere of radius $\ensuremath {k_\mathrm{f}}$ (the FERMI wave vector) contains all occupied levels and determines the electron concentration

$\displaystyle \ensuremath {k_\mathrm{f}}= \root 3 \of {3\pi^2n} \ .$

(3.48)

The values of the metal work function and $\ensuremath {k_\mathrm{f}}$ for various metals are summarized in the right part of Table 3.1 [114]. The value of $\ensuremath{{\mathcal{E}}_\mathrm{f}}- \ensuremath {{\mathcal{E}}_\mathrm{c}}$ can then directly be calculated from the carrier concentration assuming a parabolic dispersion relation and a MAXWELLian distribution function.

At the semiconductor side the height of the energy barrier is given by $\ensuremath {\mathrm{q}}\ensuremath{\Phi_\mathrm{e}}$ for electrons and $\ensuremath {\mathrm{q}}\ensuremath{\Phi_\mathrm{h}}$ for holes. Note that in the derivation of the TSU-ESAKI formula the barrier height $\ensuremath {\mathrm{q}}\ensuremath{\Phi_\mathrm{B}}$ , which denotes the energetic difference between the FERMI energy and the band edge in the dielectric, is used. Depending on the considered tunneling process, $\ensuremath {\mathrm{q}}\ensuremath{\Phi_\mathrm{B}}$ must be calculated from $\ensuremath {\mathrm{q}}\ensuremath{\Phi_\mathrm{e}}$ or $\ensuremath {\mathrm{q}}\ensuremath{\Phi_\mathrm{h}}$ .

A. Gehring: Simulation of Tunneling in Semiconductor Devices


Previous: 3.4 The Energy Barrier Up: 3.4 The Energy Barrier Next: 3.4.2 Image Force Correction