3.5 Transmission Coefficient Modeling
Now that the shape of the energy barrier has been treated, the calculation of
the quantum-mechanical transmission coefficient of such a barrier can be
investigated. The transmission coefficient 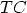 is defined as the ratio of the
quantum-mechanical current density (2.16) due to an incident wave in
Region 1 and a transmitted wave in Region N, see Fig. 3.9. The assumption of
plane waves in both regions3.5
is defined as the ratio of the
quantum-mechanical current density (2.16) due to an incident wave in
Region 1 and a transmitted wave in Region N, see Fig. 3.9. The assumption of
plane waves in both regions3.5
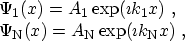 |
(3.53) |
leads to the transmission coefficient
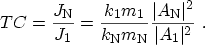 |
(3.54) |
The wave function amplitudes 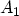 and
and
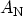 can be found by solving the
stationary SCHRÖDINGER equation (2.13) in the barrier region. This can be
achieved by various methods. The WENTZEL-KRAMERS-BRILLOUIN approximation
can be applied either analytically for a linear barrier, or numerically for
arbitrary barriers. GUNDLACH's method can be used for a single linear energy
barrier, while the transfer-matrix and quantum transmitting boundary methods
are applicable for arbitrary-shaped barriers. The transfer-matrix method can
be applied using either constant or linear potential segments as shown in
Fig. 3.9. The different methods will be described in this section and a
brief comparison at the end summarizes their advantages and shortcomings.
can be found by solving the
stationary SCHRÖDINGER equation (2.13) in the barrier region. This can be
achieved by various methods. The WENTZEL-KRAMERS-BRILLOUIN approximation
can be applied either analytically for a linear barrier, or numerically for
arbitrary barriers. GUNDLACH's method can be used for a single linear energy
barrier, while the transfer-matrix and quantum transmitting boundary methods
are applicable for arbitrary-shaped barriers. The transfer-matrix method can
be applied using either constant or linear potential segments as shown in
Fig. 3.9. The different methods will be described in this section and a
brief comparison at the end summarizes their advantages and shortcomings.
Figure 3.9:
The energy barrier of a single-layer dielectric. The
potential energy 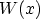 may either be the conduction band or the valence band
energy, depending on the tunneling process. The linear and constant potential
approximations refer to the transfer-matrix method described in Section 3.5.3.
may either be the conduction band or the valence band
energy, depending on the tunneling process. The linear and constant potential
approximations refer to the transfer-matrix method described in Section 3.5.3.
|
|
Subsections
A. Gehring: Simulation of Tunneling in Semiconductor Devices
![]() is defined as the ratio of the
quantum-mechanical current density (2.16) due to an incident wave in
Region 1 and a transmitted wave in Region N, see Fig. 3.9. The assumption of
plane waves in both regions3.5
is defined as the ratio of the
quantum-mechanical current density (2.16) due to an incident wave in
Region 1 and a transmitted wave in Region N, see Fig. 3.9. The assumption of
plane waves in both regions3.5![\includegraphics[width=.52\linewidth]{figures/TM}](img404.png)