|
|
|
|
Previous: 3.5.3 Transfer-Matrix Method Up: 3.5.3 Transfer-Matrix Method Next: 3.5.3.2 Piecewise-Linear Potential |
If an arbitrary potential barrier is segmented into N regions with constant
potentials (see Fig. 3.9) the wave function in each region can be written as
the sum of an incident and a reflected wave [93]
![]() with the wave number
with the wave number
![]() . The wave amplitudes
. The wave amplitudes ![]() ,
, ![]() , the
carrier mass
, the
carrier mass ![]() , and the potential energy
, and the potential energy ![]() are assumed constant for
each region
are assumed constant for
each region ![]() . With the interface conditions for energy and momentum
conservation
. With the interface conditions for energy and momentum
conservation
| (3.73) | |||
| (3.74) |
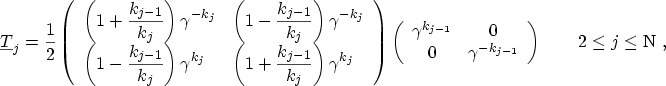 |
(3.76) |
If it is assumed that there is no reflected wave in Region N and the amplitude of the incident wave is unity, (3.77) simplifies to
A. Gehring: Simulation of Tunneling in Semiconductor Devices