|
|
|
|
Previous: 3.5.3.1 Piecewise-Constant Potential Up: 3.5.3 Transfer-Matrix Method Next: 3.5.4 Quantum Transmitting Boundary Method |
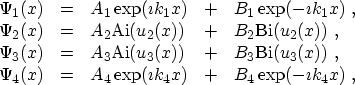 |
(3.79) |
| (3.80) |
The transfer matrices between adjacent layers are again calculated from (3.75). Using the first two equations of (3.81) and the WRONSKI an3.8 [138]
| (3.82) |
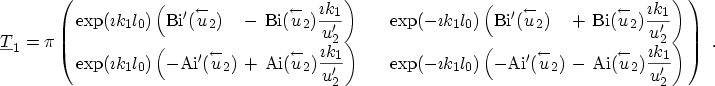 |
Using the next two lines of (3.81) yields
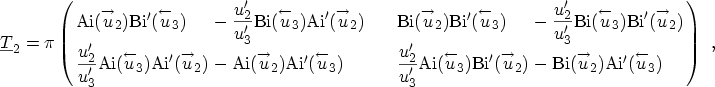 |
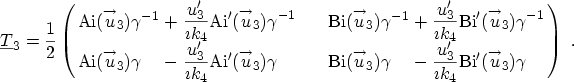 |
(3.83) |
While being more accurate than the constant potential approach this method is computationally more expensive. This drawback, however, is offset by the fact that a lower resolution and thus fewer matrix multiplications are necessary to resolve an energy barrier consisting of linear potential segments.
Simulations using the transfer-matrix method have been reported by several authors [145,146,147,148]. Others compared the constant and linear potential approaches and found the constant potential method more feasible for device simulation [149]. The main advantage of the linear-potential transfer-matrix method is, that for linear potential segments the accuracy does not depend on the resolution as it does for the constant-potential transfer-matrix method. However, the evaluation of the AIRY functions must be carefully implemented to avoid overflow.
Although the transfer-matrix method for constant or linear potential segments is intuitively easy to understand and implement, the main shortcoming of the method is that it becomes numerically instable for thick barriers. This has been observed by several authors [150,151,152,153,149]. The reason for the numerical problems is that during the matrix multiplications exponentially growing and decaying states have to be multiplied, leading to rounding errors which eventually exceed the amplitude of the wave function itself for thick barriers.
These problems have been overcome by a further segmentation of the barrier
into slices with more accurate transfer matrices [150], the use of
scattering matrices instead of transfer matrices [151], iterative
methods [152], or by simply setting the transfer matrix entries to
zero if the decay factor
![]() exceeds a certain value of about
20 [149]. In the next section a method will be presented which
avoids this problem and allows a fast and reliable transmission coefficient
estimation.
exceeds a certain value of about
20 [149]. In the next section a method will be presented which
avoids this problem and allows a fast and reliable transmission coefficient
estimation.
A. Gehring: Simulation of Tunneling in Semiconductor Devices