


Next: 2.3.3.3 Linear Capacitor
Up: 2.3.3 Devices
Previous: 2.3.3.1 Conductor
The constitutive relations for a linear temperature dependent resistor are
| V |
= |
I . R(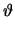 ) ) |
(2.32) |
R(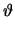 ) ) |
= |
R0 . 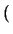 1 + 1 + 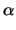 . ( . (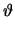 -
- 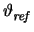 ) ) |
(2.33) |
| P |
= |
V . I |
(2.34) |
The same considerations as for conductors apply for
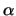
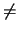 0 . The stamp is given as
0 . The stamp is given as
| yx, y |
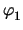 |
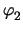 |
I |
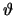 |
f |
| n1 |
|
|
1 |
|
- I |
| n2 |
|
|
-1 |
|
I |
| I |
-1 |
1 |
R |
R0 . 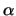 . I . I |
V - I . R |
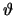 |
- I |
I |
- V |
|
P |
As the node voltages and the branch current are independent solution variables,
it is not guaranteed that the expression
V - I . R equals zero while
iterating towards the final solution. In the above stamp, the independent
solution variable for the current I can be eliminated making I a dependent
variable. The resulting stamp reads
| yx, y |
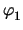 |
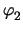 |
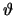 |
f |
| n1 |
G |
- G |
V . 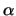 . R0 . G2 . R0 . G2 |
- I |
| n2 |
- G |
G |
- V . 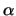 . R0 . G2 . R0 . G2 |
I |
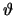 |
-2 . V . G |
2 . V . G |
I2 . 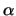 . R0 . R0 |
P |
with G = 1/R. Since I is a dependent variable, I and V may be used
interchangeably, as long as R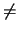 0. The above stamp is, of course, equal
to the result obtained by directly considering the conductor G = 1/R which,
in this case, depends in a non-linear way on
0. The above stamp is, of course, equal
to the result obtained by directly considering the conductor G = 1/R which,
in this case, depends in a non-linear way on 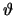 . However, the
current I can only be eliminated if R
. However, the
current I can only be eliminated if R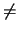 0 so that the second stamp is
somewhat more restrictive. Furthermore, this procedure shows how additional
currents can be added or eliminated whenever needed as long as a unique
inversion
V = g-1(I) of the the branch relation I = g(V) exists which is
not the case for R = 0. Of course, I must not be used by other device
models and hence be a local quantity of the device. In addition, V and I
need not necessarily be defined for the same branch as is the case for
current-controlled voltage sources.
0 so that the second stamp is
somewhat more restrictive. Furthermore, this procedure shows how additional
currents can be added or eliminated whenever needed as long as a unique
inversion
V = g-1(I) of the the branch relation I = g(V) exists which is
not the case for R = 0. Of course, I must not be used by other device
models and hence be a local quantity of the device. In addition, V and I
need not necessarily be defined for the same branch as is the case for
current-controlled voltage sources.
Another interesting application can be found when adding the branch current for a
conductor as an unknown. Neglecting temperature dependencies, the stamp reads
| yx, y |
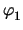 |
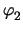 |
I |
f |
| n1 |
|
|
1 |
- I |
| n2 |
|
|
-1 |
I |
| I |
- G |
G |
1 |
V . G - I |
For an open circuit G = 0 while R = 0 results in a short circuit.
By combining the above stamp with the stamp of the ideal resistor an ideal
switch can be implemented whose stamp reads
| yx, y |
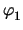 |
 |
I |
f |
| n1 |
|
|
1 |
- I |
| n2 |
|
|
-1 |
I |
| I |
- S |
S |
1 - S |
V . S - I . (1 - S) |
with S denoting the state of the switch. S = 1 gives a short circuit while S = 0
results in an open circuit.



Next: 2.3.3.3 Linear Capacitor
Up: 2.3.3 Devices
Previous: 2.3.3.1 Conductor
Tibor Grasser
1999-05-31