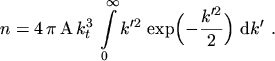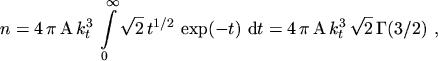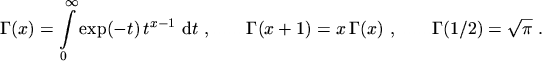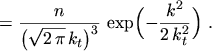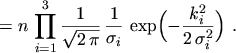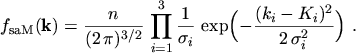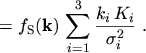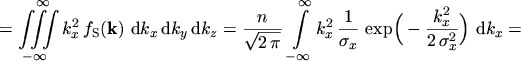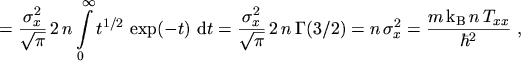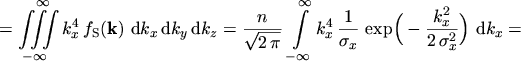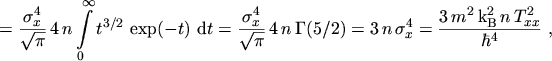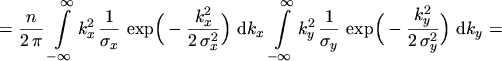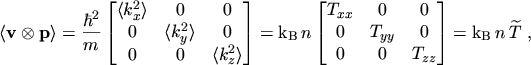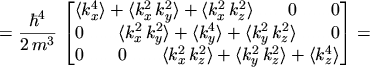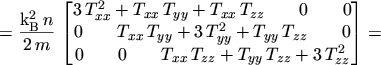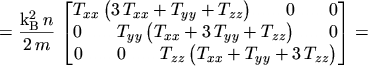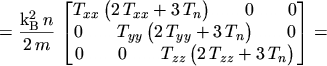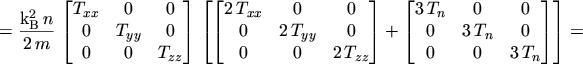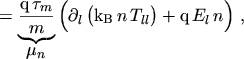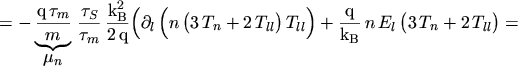In this section the flux equations of an energy transport model assuming an anisotropic distribution function will be
derived. The balance equations are not affected by an anisotropic distribution function since the tensor
quantities only appear in the odd moment equations (2.76) to
(2.78).
In order to allow for an anisotropic distribution function the starting point will be a MAXWELL
distribution
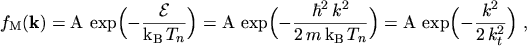 |
(5.6) |
where
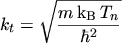 |
(5.7) |
is the standard deviation.
To get the value of the coefficient
 the normalization
the normalization
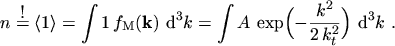 |
(5.8) |
is used. By using spherical polar coordinates and the substitution
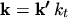 the integral can be written as
the integral can be written as
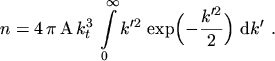 |
(5.9) |
Setting
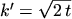 gives
gives
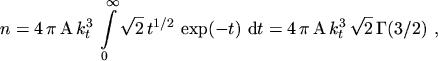 |
(5.10) |
where the GAMMA function has been used
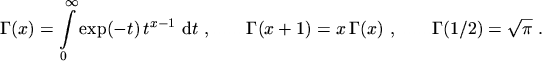 |
(5.11) |
The coefficient
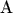 and the distribution function is found to be
and the distribution function is found to be
An anisotropic MAXWELL distribution function is obtained by splitting the argument of the
exponential function into three separate components
Since the odd moments of this distribution function are zero, current flow would not be possible. To allow
for current flow, the distribution function is shifted
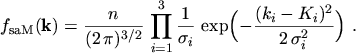 |
(5.16) |
Again, the diffusion approximation is applied which assumes that the displacement is
small,
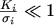 ,
,
The symmetric and the anti-symmetric part are found to be
The equations for the current density and the energy flux density are obtained by calculating
the statistical averages of the tensors occurring in
eqns. (2.76) and (2.77)
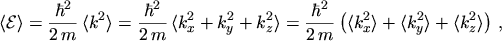 |
(5.20) |
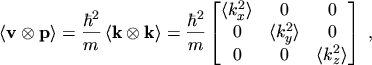 |
(5.21) |
The elements outside the trace are zero due to the symmetry properties of
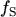 ,
introduced by the diffusion approximation. The statistical averages present in
eqns. (5.20) to (5.23) all have one of the forms
,
introduced by the diffusion approximation. The statistical averages present in
eqns. (5.20) to (5.23) all have one of the forms
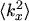 ,
,
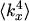 , or
, or
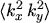 , and will be integrated in
the following.
, and will be integrated in
the following.
Inserting these results into eqns. (5.20) to (5.23)
finally yields
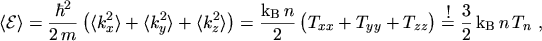 |
(5.26) |
which reflects eqn. (5.5),
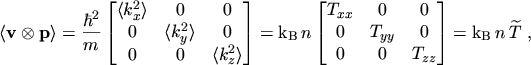 |
(5.27) |
and
The flux equations of the anisotropic energy transport model thus become
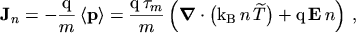 |
(5.29) |
and their one-dimensional projection onto an arbitrary direction
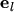 reads
reads
In terms of the general flux equation (3.41)
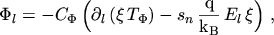 |
(5.33) |
the quantities
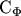 ,
, 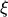 , and
, and 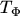 read
read
Note that the discretization eqn. (3.61) can be used without
modification.
M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF
![]() the normalization
the normalization