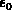 nach einer Taylorreihe zu entwickeln. Dabei erhält man
folgende, parabolische Abhängigkeit der Energie vom Wellenvektor,
nach einer Taylorreihe zu entwickeln. Dabei erhält man
folgende, parabolische Abhängigkeit der Energie vom Wellenvektor,




Die Bandstruktur von Silizium und die möglichst allgemeine Implementierung in einem Monte-Carlo-Programm ist ganz entscheidend für die physikalische Aussagekraft der ermittelten Ergebnisse. Einerseits ist die Bandstruktur im allgemeinen anisotrop und setzt sich aus mehreren Bändern sowohl des Valenz- als auch des Leitfähigkeitsbandes zusammen und erfordert bei einer vollständigen Berücksichtigung der Dynamik einen sehr hohen Speicherbedarf und einen erhöhten Rechenbedarf zur Lösung der Bewegungsgleichungen, da stets in Richtung des elektrischen Feldes interpoliert werden muß. Andererseits muß man, um den Hochenergieanteil der Elektronen möglichst genau bestimmen zu können, die Aufspaltung in einzelne Bänder berücksichtigen. Die Bandstruktur beeinflußt nicht nur die Dynamik der einzelnen Ladungsträger, sondern darüberhinaus hängen auch die Streuraten von dem quantitativen Verhalten der Zustandsdichte ab.
Wenn das Verhalten von Elektronen nur bei kleinen Energien untersucht werden
soll, so ist es ausreichend, das Leitfähigkeitsband in der Umgebung dessen
Minimums 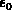 nach einer Taylorreihe zu entwickeln. Dabei erhält man
folgende, parabolische Abhängigkeit der Energie vom Wellenvektor,
nach einer Taylorreihe zu entwickeln. Dabei erhält man
folgende, parabolische Abhängigkeit der Energie vom Wellenvektor,
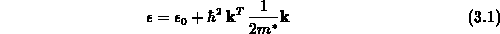
mit der effektiven Masse 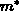 , die bei isotropen Materialeigenschaften als
, die bei isotropen Materialeigenschaften als
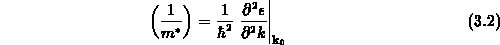
gegeben ist. Wählt man nun das Minimum des Leitfähigkeitsbandes als relativen
Bezugspunkt, so kann 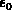 Null gesetzt werden. Eine sehr effiziente
Erweiterung dieses Einbandmodells findet sich bei [53]. Mithilfe einer
Störungsrechnung [53][54][55][56] kann folgende
Näherung für die Energierelation
Null gesetzt werden. Eine sehr effiziente
Erweiterung dieses Einbandmodells findet sich bei [53]. Mithilfe einer
Störungsrechnung [53][54][55][56] kann folgende
Näherung für die Energierelation
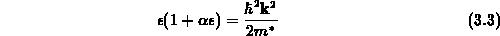
geschrieben werden, sodaß sich eine nichtparabolische Abhängigkeit ergibt. Die
Konstante 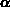 wird als Nichtparabolizitätskonstante bezeichnet und kann
näherungsweise mit der Bandlücke
wird als Nichtparabolizitätskonstante bezeichnet und kann
näherungsweise mit der Bandlücke 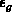 zwischen den Valenzband und dem
Leitfähigkeitsband
zwischen den Valenzband und dem
Leitfähigkeitsband
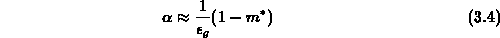
bestimmt werden.
In Silizium ist das Minimum des Leitfähigkeitsbandes nicht im
Mittelpunkt der Brillouinzone lokalisiert. Man spaltet die effektive Masse
des Elektrons in eine longitudinale 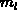 und eine transversale Komponente
und eine transversale Komponente 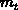 auf, sodaß die Energie nun mit der Bandformfunktion
auf, sodaß die Energie nun mit der Bandformfunktion 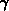 als
als
geschrieben werden kann, wobei die effektive Masse nun als Tensor definiert ist,
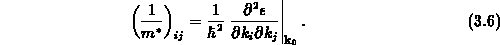
Man kann also Gleichung 3.5 auch in Tensorschreibweise
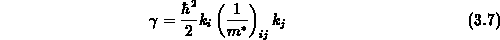
angeben, wobei
Zur Berechnung von hochenergetischen Elektronen ist dieses Verfahren nicht geeignet. Entweder bezieht man die volle anisotrope Bandstruktur mit ein, oder man entwickelt analytische Mehrbandmodelle, die im wesentlichen die Merkmale der Zustandsdichte in Silizium enthalten. Damit erreicht man, daß zwar die Dynamik der Elektronen nur isotrop berücksichtigt wird, jedoch die Abgeschlossenheit der einzelnen Bänder in bezug auf den Wellenvektor erhalten bleibt. Da die Zustandsdichte
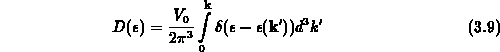
in die Streuraten eingeht, wird bei einem Einbandmodell im Hochenergiebereich die Streurate schwer überschätzt.
Ein analytisches Modell, das ein nichtparabolisches und drei
parabolische Bänder auswertet, ist von R. Brunetti et al.
[58] entwickelt worden. Die Nachbildung der Zustandsdichte mit
mehreren, isotropen numerischen Bändern ist in [59]
beschrieben. Ausgehend von dem Argument, daß, wenn man viele
Elektronen mit einem Vielteilchen-Monte-Carlo-Algorithmus verfolgt,
die Anisotropieeffekte einer Bandstruktur nahezu vernachlässigbar
sind, beziehungsweise nicht stark ins Gewicht fallen, ist in
[51][60] ein Verfahren dargestellt, mit dem sowohl die
Zustandsdichte als auch die Ableitung der Energierelation numerisch
behandelt wird. Dabei wird eine isotrope Gruppengeschwindigkeit
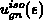 zugleich mit einer isotropen Zustandsdichte
zugleich mit einer isotropen Zustandsdichte
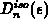
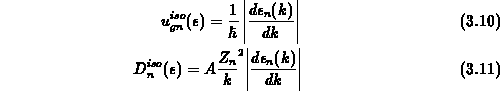
gelöst [51], wobei sich der Index  auf ein Band bezieht. In dieser
Gleichung ist
auf ein Band bezieht. In dieser
Gleichung ist 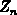 die Multiplizität eines Bandes und
die Multiplizität eines Bandes und 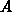 ein
Proportionalitätsfaktor. Da in dieser Darstellung zwei
Differentialgleichungen für eine einzige Lösungsfunktion auftreten, sucht
man mit einem willkürlichen Gewichtsfaktor
ein
Proportionalitätsfaktor. Da in dieser Darstellung zwei
Differentialgleichungen für eine einzige Lösungsfunktion auftreten, sucht
man mit einem willkürlichen Gewichtsfaktor  eine Lösung derart, daß der
relative Fehler
eine Lösung derart, daß der
relative Fehler 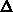 minimiert wird. Man muß also diesen Fehler in der
folgenden Beziehung mit der realen Zustandsdichte und Gruppengeschwindigkeit
minimiert wird. Man muß also diesen Fehler in der
folgenden Beziehung mit der realen Zustandsdichte und Gruppengeschwindigkeit
mit den zusätzlichen Bedingungen minimieren:
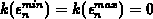 , wobei
, wobei 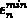 und
und
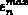 die jeweiligen Schranken des isotropen Bandes sind.
die jeweiligen Schranken des isotropen Bandes sind.
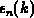 ist monoton steigend im Intervall
ist monoton steigend im Intervall
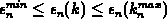 , und
, und 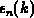 ist monoton fallend im Intervall
ist monoton fallend im Intervall 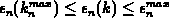 .
.
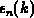 ist stetig an der Stelle
ist stetig an der Stelle 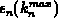 .
.
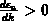 und eines dem Fall
und eines dem Fall 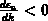 entspricht.
entspricht.
Die Anordnung von Silizium in der Einheitszelle eines kubisch
flächenzentriertem Gitter ist in Abbildung 3.1 veranschaulicht. Die
Brillouinzone eines kubisch flächenzentrierten Gitters ist in
Abbildung 3.2 mit den wichtigsten Symmetriepunkten und -achsen
dargestellt und aus [41] entnommen. Der Punkt 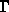 repräsentiert
den Mittelpunkt, lateinische Buchstaben einzelne Punkte an der
Begrenzungsfläche und die griechischen Symbole stehen für die
Symmetrieachsen. Die Koordinate des Punktes
repräsentiert
den Mittelpunkt, lateinische Buchstaben einzelne Punkte an der
Begrenzungsfläche und die griechischen Symbole stehen für die
Symmetrieachsen. Die Koordinate des Punktes 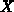 beträgt
beträgt
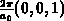 mit der Gitterkonstanten
mit der Gitterkonstanten 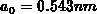 . Eine
anisotrope Vollbandstruktur und ein isotropes, aus sechs kugelsymmetrischen
Leitfähigkeitsbändern bestehendes Mehrbandmodell, dessen Gewichtsfaktor
. Eine
anisotrope Vollbandstruktur und ein isotropes, aus sechs kugelsymmetrischen
Leitfähigkeitsbändern bestehendes Mehrbandmodell, dessen Gewichtsfaktor
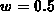 beträgt, sind in Abbildung 3.3 und 3.4 gegeben. Die
Daten einer anisotropen Bandstruktur mit empirischen Pseudopotentialen für eine
kubisch flächenzentrierte Symmetrie von Silizium sind [57][61]
entnommen. Eine genaue Diskussion, inwieweit Spin-Bahn-Kopplung, nichtlokale
Pseudopotentiale oder Hybridisierung die Bandstruktur beeinflussen, findet sich
in [62][63][64]. Eine Zusammenfassung von
Bandstrukturberechnungen von verschiedenen kristallinen und amorphen Materialien
ist in [65] gegeben.
beträgt, sind in Abbildung 3.3 und 3.4 gegeben. Die
Daten einer anisotropen Bandstruktur mit empirischen Pseudopotentialen für eine
kubisch flächenzentrierte Symmetrie von Silizium sind [57][61]
entnommen. Eine genaue Diskussion, inwieweit Spin-Bahn-Kopplung, nichtlokale
Pseudopotentiale oder Hybridisierung die Bandstruktur beeinflussen, findet sich
in [62][63][64]. Eine Zusammenfassung von
Bandstrukturberechnungen von verschiedenen kristallinen und amorphen Materialien
ist in [65] gegeben.
Die Zustandsdichte und die Gruppengeschwindigkeit verschiedener Modelle für die
Bandstruktur sind in Abbildung 3.5 und 3.6 verglichen. Dabei
sind diese Größen mit einem einzelnen parabolischen, einem einzelnen
nichtparabolischen Bandmodell, einem isotropen Mehrbandmodell als auch mit
einem anisotropen Vollbandmodell [66] berechnet worden. Bei den
Einbandmodellen ist die effektive Masse als 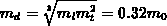 mit
mit 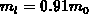 und
und 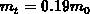 gegeben
[23][41]. Zusätzlich beträgt die Nichtparabolizität
gegeben
[23][41]. Zusätzlich beträgt die Nichtparabolizität
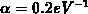 . Es zeigt sich, daß ein parabolisches Band nur im Minimum
des jeweiligen Bandes mit einem realen Bandmodell übereinstimmt. Eine
Erweiterung auf Nichtparabolizität kann bis zum ersten Maximum bei ungefähr
. Es zeigt sich, daß ein parabolisches Band nur im Minimum
des jeweiligen Bandes mit einem realen Bandmodell übereinstimmt. Eine
Erweiterung auf Nichtparabolizität kann bis zum ersten Maximum bei ungefähr
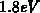 der tatsächlichen Zustandsdichte als geeignete Näherung verwendet
werden. Die Gruppengeschwindigkeit
der tatsächlichen Zustandsdichte als geeignete Näherung verwendet
werden. Die Gruppengeschwindigkeit 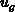 wird deutlich unterschätzt, je
größer die Nichtparabolizität gewählt wird, da im Gegensatz zum parabolischen
Einbandmodell noch ein zusätzlicher Divisor auftritt,
wird deutlich unterschätzt, je
größer die Nichtparabolizität gewählt wird, da im Gegensatz zum parabolischen
Einbandmodell noch ein zusätzlicher Divisor auftritt,
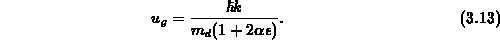
Eine gute Näherung sowohl für die Zustandsdichte als auch für die
Gruppengeschwindigkeit kann also nur dann erzielt werden, wenn der
Nichtparabolizitätsparameter klein ist oder der effektiven Masse
Tensoreigenschaften (Gleichung 3.8) zugeordnet werden. Hingegen
wird bei einem isotropen Mehrbandmodell Zustandsdichte und
Gruppengeschwindigkeit bis zu  richtig reproduziert. Da bei der
Berechnung des Hochenergieanteils der Elektronen die Zustandsdichte bei den
Streuraten Eingang findet und auch die Gruppengeschwindigkeit des isotropen
Mehrbandmodell mit der realen übereinstimmt, ist mit einem isotropen
Mehrbandmodell ein vertretbarer Kompromiß zwischen numerischer Effizienz und
physikalischer Genauigkeit gegeben.
richtig reproduziert. Da bei der
Berechnung des Hochenergieanteils der Elektronen die Zustandsdichte bei den
Streuraten Eingang findet und auch die Gruppengeschwindigkeit des isotropen
Mehrbandmodell mit der realen übereinstimmt, ist mit einem isotropen
Mehrbandmodell ein vertretbarer Kompromiß zwischen numerischer Effizienz und
physikalischer Genauigkeit gegeben.



