A reasonable refinement technique can be obtained from a sufficient criterion for the connection of two given points by a Delaunay edge. If this sufficient condition is not fulfilled, the boundary edge connecting the two points may not be reproduced in the subsequent triangulation step which hence calls for a refinement of that edge. If the sufficient condition is fulfilled (i.e. if the refinement criterion fails), the edge will be created by the Delaunay triangulation.
PROOF. By definition of the Delaunay triangulation, the circumcircle
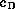of a Delaunay triangle (A B C) does not contain any
other point of 
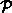in its interior. If the two given points
A and B are
connected by a Delaunay edge, then they must be part of a Delaunay
triangle and hence a circumcircle which does not contain
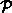any other point of in its interior must exist.
If we assume that the two points A and B are not
connected by a Delaunay edge there must not be a circle
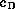passing through A and B and through a
third point C of 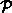without containing
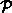another point of in its interior. But as there exists a
circle c passing through A and B which does not
contain any other node of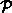
neither on its interior, nor on its boundary, it is also possible to
construct a circle 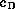with the same properties as c
except for passing through a third point of 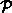, which
contradicts the assumption
.
The following theorem yields a sufficient (but not necessary) criterion which is much easier to verify numerically, and which is finally employed by VORONOI.
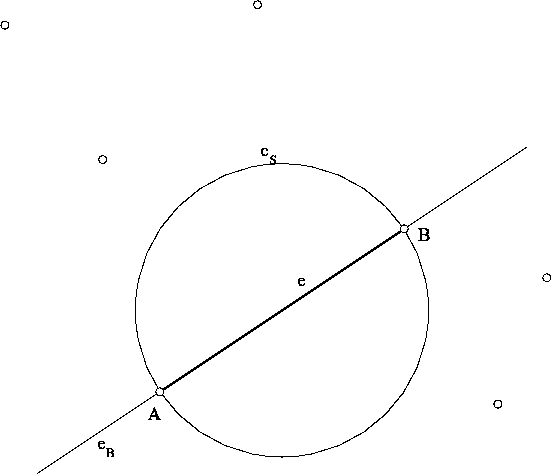
Figure 6.16: All grid points lie outside the smallest circle
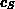passing through A and B, hence the edge 
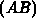is a Delaunay
edge.
PROOF.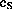 
is a special instance of
a circle c of theorem 6.5 and hence the existence
of 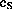is sufficient (but not necessary) for the existence
of the Delaunay edge connecting A and B.
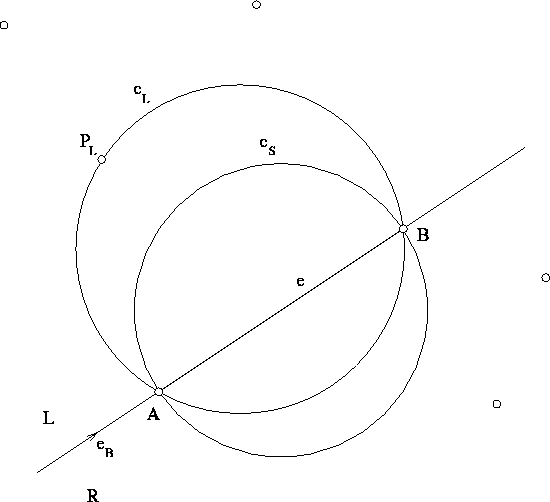
Figure 6.17: Proof of the boundary refinement criterion
There is another, more intuitive approach to define and understand the boundary refinement criterion, based on the construction in Figure 6.17.
PROOF. Let us first assume that there exists the smallest
circle 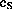passing through A and B which does not
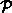contain any other point of in
its interior, but that there is no edge connecting A
and B in the Delaunay triangulation of the point set .
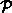Of all points in , let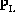 
be the closest point in the
left half-plane L (this ``closest point'' leads to a circle
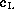so that no other point of 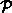in the left half-plane
lies inside 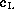). As can be seen from Figure 6.17, there
are no other points in the right half-plane that lie inside
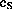, so (
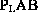) is a Delaunay triangle, hence the
edge connecting A and B exists, in contradiction
to the assumption.
The negation of Theorem 6.6 leads to the desired refinement criterion. Every boundary edge that does not fulfill Theorem 6.6 must be refined by insertion of an additional boundary grid point.
