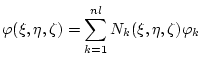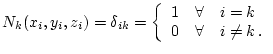5.1 Berechnung der Stromdichteverteilung
Die Methode der Finiten Elemente (FEM) [133,134] basiert auf einer
numerischen Näherung der Lösung (der partiellen Differentialgleichungen)
durch gewichtete Summierung von Formfunktionen auf einem geometriekonformen
Gitter. Formfunktionen5.1 sind in der Regel den Gitterpunkten zugeordnet und
werden so gewählt, dass am Rand zumindest die Dirichlet-Bedingungen exakt
erfüllt sind. Falls bei der Finiten Elemente Methode keine Randbedingungen
an Gebietsrändern vorgegeben werden, erfüllen diese automatisch homogene
Neumann-Bedingungen (natürliche Randbedingungen). Da die Leiteroberfläche
bis auf die Kontakte einen homogenen Neumann-Rand entspricht, läßt sich dies
für die Stromdichteberechnung vorteilhaft nutzen, weil keine spezielle
Behandlung des größten Teils der Leiteroberfläche erforderlich ist.
Die Berechnung der Stromdichte erfolgt auf einem Tetraedergitter, weil damit
beliebige Geometrien behandelt werden können. Dazu bedarf es zuerst der
Lösung der Euler-Gleichung (3.53) innerhalb der leitfähigen Segmente
unter Berücksichtigung der möglichen Randbedingungen
(vergl. Abschnitt 3.1.2). Die Lösung des diskretisierten Gleichungssystems wird meist mit einem iterativen
Gleichungslösungsverfahren ermittelt: Das konjugierte
Gradientenverfahren5.2 (CG) [135] zeichnet sich dadurch aus, dass es
nahezu keinen zusätzlichen Speicherplatz benötigt und im Regelfall mit
deutlich weniger Rechenoperationen auskommt als z.B. die Gaußsche Elimination.
Das exakte Verfahren liefert die Lösung eines Gleichungssystems in n
Unbekannten nach höchstens n Schritten [136], wenngleich auch bei der Berücksichtigung der Rundungsfehler das Verfahren nicht immer konvergieren muss.
Aus dem elektrischen Potenzial 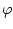 erhält man die elektrische
Feldstärke
erhält man die elektrische
Feldstärke
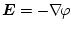 , in weiterer Folge ergibt sich durch
das lokale Ohmsche Gesetz
, in weiterer Folge ergibt sich durch
das lokale Ohmsche Gesetz
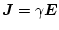 die
Stromdichteverteilung.
die
Stromdichteverteilung.
Erwähnenswert erscheint in diesem Zusammenhang noch die Diskretisierung des Potenzials, das entweder über eine lineare Variation
allgemein durch
ausgedrückt werden kann, oder für eine quadratische Variation des
Potenzials im Element mittels eines quadratischen Polynoms:
Aus diesen Formulierungen erkennt man, dass entweder 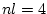 oder
oder 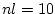 Elementsknoten benötigt werden. Sind die Koeffizienten
Elementsknoten benötigt werden. Sind die Koeffizienten 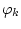 in
allen Knoten eines Elementes bestimmt, so kann der Potenzialwert für einen
beliebigen Punkt
in
allen Knoten eines Elementes bestimmt, so kann der Potenzialwert für einen
beliebigen Punkt
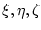 innerhalb des Elements durch Approximation
mittels der Formfunktionen
innerhalb des Elements durch Approximation
mittels der Formfunktionen 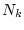
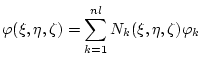 |
(5.6) |
gefunden werden. Danach wird der Gradientoperator ausgewertet und mittels der
elektrischen Feldstärke über das lokale Ohmsche Gesetz die Stromdichte
ermittelt.
Die Berechnung des Gradienten erfolgt analytisch durch Ableitung der
Ansatzfunktionen nach den Ortskoordinaten.
Fußnoten
- ...
Formfunktionen5.1
-
Formfunktionen besitzen die spezielle Interpolationseigenschaft an Knoten,
z.B. am Knoten
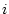 gilt:
gilt:
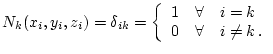 |
(5.3) |
Mit dieser Eigenschaft der lokalen Formfunktionen stellen die Knotenelemente
die Stetigkeit des elektrischen Potenzials beim Elementsübergang sicher.
Außerdem wird von den Formfunktionen gefordert, dass sie voneinander
unabhängig sind und aus dem Raum der stückweise stetigen einfach
differenzierbaren Funktionen stammen. Dabei ist noch anzumerken, dass sich
die globale Formfunktion
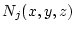 aus den lokalen Formfunktionen der am
Knoten
aus den lokalen Formfunktionen der am
Knoten 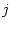 angrenzenden Tetraederelemente zusammensetzt.
angrenzenden Tetraederelemente zusammensetzt.
- ...
Gradientenverfahren5.2
- Voraussetzung für den Einsatz von CG ist eine symmetrische und positiv
definite Systemmatrix.
C. Harlander: Numerische Berechnung von Induktivitšten in dreidimensionalen Verdrahtungsstrukturen
![]() erhält man die elektrische
Feldstärke
erhält man die elektrische
Feldstärke
![]() , in weiterer Folge ergibt sich durch
das lokale Ohmsche Gesetz
, in weiterer Folge ergibt sich durch
das lokale Ohmsche Gesetz
![]() die
Stromdichteverteilung.
die
Stromdichteverteilung.