2.3 Die Methode von Nanz

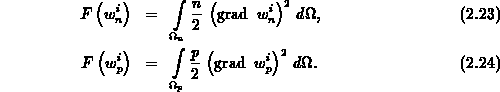
Die Freiheit in der Wahl der Gewichtsfunktionen ermöglicht eine Berücksichtigung der in Abschnitt 2.2 beschriebenen numerischen Probleme. Die Tatsache, daß die Elektronenstromdichte in Gebieten mit hoher Elektronenkonzentration, die Löcherstromdichte in Gebieten mit hoher Löcherkonzentration ungenau ist, legt nahe, für jede der Leitungsstromdichten eigene, also für Elektronen und Löcher getrennte Gewichtsfunktionen zu verwenden. Als Regel gilt, daß die Kontaktstrom-Integration Beiträge aus Gebieten, in denen eine genaue Berechnung der Stromdichten nicht möglich ist, also in Gebieten mit hohen Ladungsträgerkonzentrationen, ausschließen muß. Diese Forderung läßt sich als Gütefunktional für die beiden Typen von Gewichtsfunktionen formulieren: Gewichtsfunktionen für Elektronen bzw. Löcher, deren Gradienten - denn nur diese gewichten die Stromdichten - in Gebieten hoher Ladungsträgerkonzentrationen minimal sind, minimieren die Funktionale

Gewichtsfunktionen, die die Funktionale (2.23)-(2.24) global minimieren, haben ein minimales Betragsquadrat der Gradienten in Gebieten mit hohen Ladungsträgerkonzentrationen.
Hinreichende Bedingungen für ein Extremum der 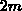Funktionale sind neben homogenen Neumann-Randbedingungen auf dem Neumann-Teilbereich (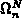 und 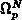) die Euler-Lagrangegleichungen für =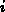

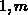
Die Lösungen dieser linearen partiellen Differentialgleichungen sind die optimalen Gewichtsfunktionen für den Elektronen- bzw. Löcherstrom.
Die Diskretisierung der Gleichungen (2.25)-(2.26) wurde in [73] abgeleitet. Die dort präsentierten Ausdrücke für die Interpolation können vereinfacht und numerisch robust implementiert werden. Die ,,Scharfetter-Gummel``-Diskretisierung dieser Gleichungen ist ein Lehrbuchbeispiel für das Prinzip der harmonischen Mittelung, auf dem diese Interpolationsmethode beruht. Deshalb soll die Diskretisierung der Gleichung (2.25) im Licht dieses Prinzips skizziert werden. Die Diskretisierung der Gleichung für die Löcher-Gewichtsfunktionen (2.26) ist dazu analog.
Als Vorbemerkung sei erwähnt, daß sich die Euler-Lagrangegleichungen (2.25)-(2.26) hinsichtlich ihrer mathematischen Eigenschaften recht ähnlich den Kontinuitätsgleichungen verhalten. Man denke sich etwa ein beliebiges Halbleiter-Bauelement im thermodynamischen Gleichgewicht. Die Elektronen- bzw. Löcherkonzentrationen sind dann ausschließlich vom elektrostatischen Potential exponentiell abhängig. Die Euler-Lagrangegleichungen der Gewichtsfunktionen lauten für diesen Fall

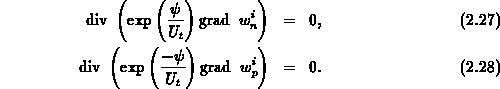
Diese Gleichungen sind identisch mit Kontinuitätsgleichungen in den Slotboom-Variablen [94]. Man beachte jedoch den unterschiedlichen Zahlenbereich. Während die Slotboom-Variablen in praktischen numerischen Anwendungen aufgrund ihres sehr großen Zahlenumfangs nur sehr beschränkte Anwendung finden, ist der Zahlenbereich der Gewichtsfunktionen 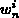, 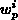mit 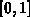eingeschränkt.
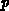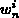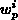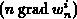Die räumlich starken Variationen von und bedingen entsprechenden Variationen in und . Eine stabile Diskretisierung muß diesem Verhalten Rechnung tragen. Zentrale Differenzen zur Approximation der Mittenwerte von und 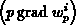sind in solchen Fällen ungeeignet. Die Scharfetter-Gummel-Interpolation bedient sich hingegen des harmonischen Mittelwertes. Der harmonische Mittelwert 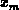zweier Zahlen 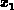und 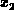ist gegeben durch

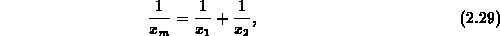
und für eine Funktion 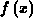auf dem Intervall 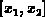durch

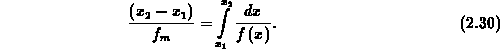
Zur Mittenwertapproximation der Ausdrücke 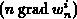und 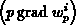auf den Intervallen 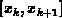, 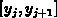zieht man für und 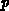eindimensionale, analytische Lösungen des Randwertproblems der Kontinuitätsgleichungen für und 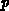heran. Es sind dies für das Intervall 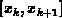mit 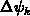= 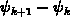elementare Exponentialfunktionen

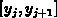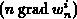Vollständig analoge Ausdrücke findet man für das Intervall in y-Richtung. Die Mittenwerte von und 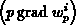ergeben sich mit Hilfe der harmonischen Mittelwerte von und 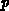auf dem Intervall 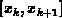zu

Nach Ausführung der bestimmten Integration und Umformung findet man mit Hilfe der Bernoullifunktion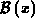

Die endgültige Diskretisierung der Euler-Lagrangegleichungen (2.25)-(2.26) erfolgt wie üblich unter Anwendung des Integralsatzes von Gauß durch Oberflächenintegration über jedes finite Volumenelement. Das resultierende lineare Gleichungssystem ist naturgemäß symmetrisch, positiv definit und schwach diagonaldominant, die Koeffizientenmatrix ist somit eine schwache 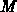-Matrix [114].
Die Methode von Nanz liefert erwartungsgemäß genaue Ergebnisse bei der Integration der Leitungsstromdichten 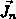und 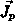. Siehe Abschnitt 2.5 mit den hierin angeführten Beispielen. Gemäß (2.8)-(2.10) treten zusätzlich zu den Vektoranteilen Skalaranteile auf, deren Integrand proportional zu den Rekombinationsraten und zu den zeitlichen Ableitungen der Ladungsträgerkonzentrationen ist. Die numerischen Ungenauigkeiten in diesen Größen gehen mit 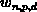entsprechend gewichtet in diese Skalaranteile ein. Die recht aufwendig erlangte Genauigkeit bei der Integration der Leitungsstromdichten wird hier wieder vermindert (siehe Abschnitt 2.5). Die Größe dieser numerischen Ungenauigkeiten ist abhängig vom Zeitschritt 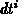und von den Ladungsträgerkonzentrationen. Dieser Nachteil der Methode von Nanz kann beseitigt werden, wenn für alle drei Stromdichten - also auch für den Verschiebungsstrom - die gleiche Gewichtsfunktion 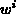verwendet wird. Die Skalarkomponenten verschwinden in diesem Fall und brauchen erst gar nicht berechnet werden. Ein weiterer Vorteil einer solchen Vorgangsweise ist, daß die Berechnung getrennter Gewichtsfunktionen für beide Ladungsträger nicht mehr notwendig ist. Der Rechenaufwand der Methode von Nanz, der im transienten Fall nicht unterschätzt werden darf, wird dadurch mehr als halbiert.
Einige Bemerkungen, den Verschiebungsstrom betreffend, sollen an dieser Stelle noch angefügt werden. Nanz schlägt vor, zur Berechnung der Verschiebungsströme ebenfalls Gewichtsfunktionen zu verwenden, nämlich Lösungen der Laplacegleichung

Die Laplacegleichung muß natürlich auch in Oxidgebieten gelöst werden, der Aufwand dafür ist verglichen mit den Gewichtsfunktionen der Leitungsstromdichten höher. Allerdings brauchen diese Funktionen nur einmal am Anfang bzw. nach jeder Gitteränderung berechnet werden. Die Vektorkomponente des Verschiebungsstroms für den Kontakt 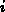ergibt sich nach Anwendung des Integralsatzes von Gauß unter der Voraussetzung eines zeitlich konstanten zu

Der zweite Term in (2.38) verschwindet im gesamten Definitionsgebiet aufgrund von Gleichung (2.37). Der erste Term in (2.38) ist nur vom zeitlichen Verlauf des Kontaktpotentials am Kontakt 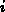abhängig. Bleibt jenes zwischen zwei Zeitschritten konstant, so verschwindet die Vektorkomponente vollständig (siehe auch Abschnitt 2.6.1). Wie bereits erläutert hat diese Methode den systematischer Nachteil, daß die Ungenauigkeiten in den Zeitableitungen der Ladungsträgerkonzentrationen durch die Skalaranteile auch in den Verschiebungsstrom eingehen.
Im Grunde genommen besteht keine Notwendigkeit, besondere Gewichtsfunktionen zur Berechnung des Verschiebungsstromes zu verwenden. Bei der Berechnung der Verschiebungsstromdichte treten keinerlei Rundungsprobleme auf, da die Werte des elektrischen Potentials von moderater Größenordnung sind und deswegen die Bildung des zeitlichen Differenzenquotienten einen vernachlässigbaren Rundungsfehler liefert. Das Oberflächenintegral liefert für den Verschiebungsstrom gute Ergebnisse. Es liegt daher nahe, für alle Teilströme, 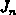, 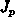und 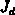die gleiche Gewichtsfunktionen 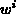zu verwenden. Bei dieser Wahl verschwinden alle Skalarkomponenten im Gesamtstrom, und in Folge alle Rundungsfehler, die in diesen Komponenten enthalten sind. Diese und weiterführende Überlegungen spielen eine zentrale Rolle in einer neuen, im Rahmen dieser Arbeit entstandenen Kontaktstrom-Integrationsmethode, die im Abschnitt 2.4 erläutert wird.