Die Matrix-Assemblierung zur Lösung der diskreten
Euler-Lagrangegleichungen
(2.25)-(2.26)
bzw. (2.40)
gewinnt an Effizienz, wenn die Symmetrie der Koeffizientenmatrix
berücksichtigt wird.
Für die Euler-Lagrangegleichungen der Elektronen- und
Löcher-Gewichtsfunktionen in der Methode von Nanz
können grundsätzlich dieselben Unterprogramme benutzt werden.
Der einzige Unterschied in den Matrixkoeffizienten entsteht,
abgesehen von den Dichten 
und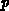 
, durch das
negative Vorzeichen des Potentialinkrementes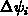 
bei der Löchergleichung in (2.36).
Das lineare Gleichungssystem mit spärlich besetzter
Koeffizientenmatrix kann iterativ gelöst werden.
Das robusteste und auf Skalarrechnern zweifellos effizienteste iterative
Lösungs-Verfahren hiezu ist ICCG [63]. Ein
entsprechendes Unterprogramm für die Lösung der
ebenfalls symmetrischen diskreten Poissongleichung
steht in der Regel im Bauelement-Simulator zur Verfügung.
Von wesentlichem Interesse ist die Frage nach der Bedingung für
den Abbruch der linearen Iteration. Während direkte
Lösungs-Verfahren gutkonditionierte lineare Gleichungssysteme
- um solche handelt es sich -
bis auf Maschinengenauigkeit lösen, bricht ein iteratives
Lösungs-Verfahren nach Erreichen einer vorgegebenen
Residuennorm ab. Auf die Frage nach der Auswirkung eines
Residuums vorgegebener Norm 
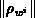der Gewichtsfunktion
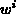auf die Genauigkeit der Kontaktstrom-Berechnung
wurde in der vorliegenden Arbeit nicht eingegangen.
Qualitativ ist zu bemerken, daß das Residuum des linearen
Gleichungssystems Maxima an den Singularitäten aufweist.
Gerade an diesen Stellen treten in der Regel
hohe Stromdichten auf, was insbesondere
für den Verschiebungsstrom gilt (Spitzenwirkung).
Eine gewisse Empfindlichkeit der Kontaktströme
bezüglich der Genauigkeit der Gewichtsfunktionen
sollte daher bemerkbar sein.
Aufgrund der Schwierigkeit der Analyse solcher
Effekte werden in der vorliegenden Arbeit die
Euler-Lagrangegleichungen direkt, durch Gaußsche Elimination,
gelöst.
Für moderat komplexe Rechengitter in zwei Dimensionen
ist ein iteratives Verfahren nicht wesentlich schneller,
unter Umständen - abhängig vom Abbruchkriterium -
sogar langsamer.
Das gilt nicht für den dreidimensionalen Fall,
wo zur iterativen Lösung der
auftretenden linearen Gleichungssysteme
extrem hohen Ranges zur Zeit keine Alternative existiert.
Eine Gewichtsfunktion pro Teilstromdichte
ergibt sich aus der Vollständigkeitsrelation (2.7).
Das hat neben der Rechenzeitersparnis den Nebeneffekt,
daß die Bedingung (2.7) exakt erfüllt ist.
Der Frage, für welchen Kontakt die Gewichtsfunktion aus
der Bedingung (2.7) berechnet werden soll,
kommt keine wesentliche Bedeutung zu.
Aus Symmetriegründen kann z.B. für Substrat-MOSFETs
die Gewichtsfunktion für den Substratkontakt auf diese
Art gewonnen werden. Noch einfacher ist, auf die Berechnung
dieser Gewichtsfunktion zu verzichten und den
in Frage stehenden Kontaktstrom
aus der Stromsummenbedingung
gemäß (2.17)-(2.19) zu berechnen.