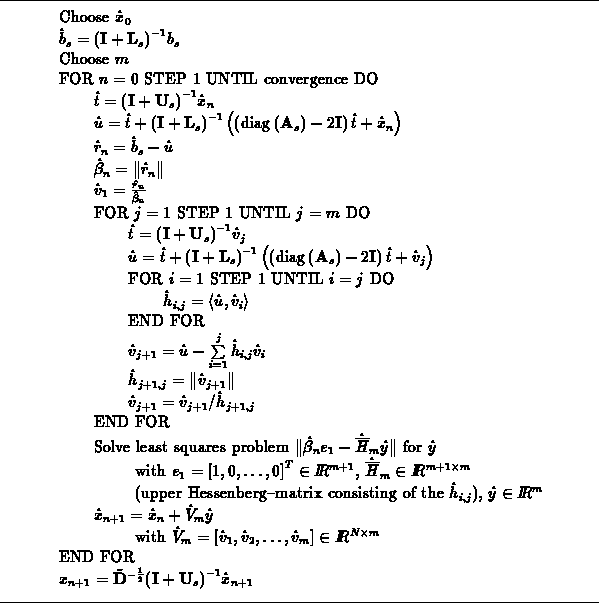
Tabelle 5.2: ILU-GMRES(
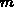 )
)




Die Generalized Minimal Residual-Methode [90]
ist streng genommen
kein iteratives Lösungs-Verfahren.
GMRES ist eine Methode, die Lösung
eines Gleichungssystems aus einem Satz orthogonaler Basisvektoren
zu bilden. Diese Vektoren werden durch einen Arnoldi-Prozeß [3]
rekursiv erzeugt. Mit jedem Iterationsschritt
wird diese Basis um einen Vektor vergrößert.
Ist 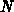 der Rang des Gleichungssystems, so liegt
in exakter Arithmetik nach maximal
der Rang des Gleichungssystems, so liegt
in exakter Arithmetik nach maximal 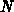 -Iterationen die
exakte Lösung des Gleichungssystems vor, allerdings
ist auch die Dimension des Raums der orthogonalen
Vektoren auf
-Iterationen die
exakte Lösung des Gleichungssystems vor, allerdings
ist auch die Dimension des Raums der orthogonalen
Vektoren auf 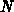 gewachsen.
Diese Basisvektoren benötigen
einen gleich großen Speicherplatz wie eine dicht besetzte Matrix.
GMRES ist in dieser Form ein direktes Lösungs-Verfahren
und nicht anwendbar auf Probleme sehr hoher Dimension.
gewachsen.
Diese Basisvektoren benötigen
einen gleich großen Speicherplatz wie eine dicht besetzte Matrix.
GMRES ist in dieser Form ein direktes Lösungs-Verfahren
und nicht anwendbar auf Probleme sehr hoher Dimension.
GMRES besitzt gemäß seiner Konzeption eine Optimalitätseigenschaft,
da bei jedem Iterationsschritt die 2-Norm des Residuums minimiert
wird, was auf ein Hessenberg-Problem kleinster Quadrate führt.
Das Minimierungsproblem kann lehrbuchmäßig durch
Givens-Rotationen oder Householder-Transformationen stabil
gelöst werden. Aufgrund dieser Minimierungseigenschaft
ist die Konvergenz von GMRES monoton.
Da für die Arnoldi-Vektoren nicht unbegrenzt
Speicherplatz zur Verfügung steht, ist es üblich, die
Iteration neu zu starten, wobei die vorher erreichte Näherungslösung
als Startwert in die neue Iteration eingeht.
Ist z.B. 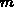 der vorzugebende maximale Rang des Arnoldi-Raumes, so schreibt
man GMRES(
der vorzugebende maximale Rang des Arnoldi-Raumes, so schreibt
man GMRES(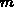 ), um anzudeuten, daß eine neugestartete
Version von GMRES benutzt wird.
Die ganze Zahl
), um anzudeuten, daß eine neugestartete
Version von GMRES benutzt wird.
Die ganze Zahl 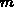 wird als Neustart-Frequenz bezeichnet.
GMRES(
wird als Neustart-Frequenz bezeichnet.
GMRES(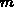 ) minimiert ebenfalls die
) minimiert ebenfalls die  -Norm des Residuums,
deswegen ist die Konvergenz ebenfalls monoton, allerdings
ist die Konvergenz naturgemäß langsamer als die direkte
Form von GMRES.
In der Praxis der Bauelement-Simulation
hat sich ein Wert von
-Norm des Residuums,
deswegen ist die Konvergenz ebenfalls monoton, allerdings
ist die Konvergenz naturgemäß langsamer als die direkte
Form von GMRES.
In der Praxis der Bauelement-Simulation
hat sich ein Wert von 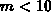 bewährt, doch können
für schlecht konditionierte Probleme auch wesentlich
größere
bewährt, doch können
für schlecht konditionierte Probleme auch wesentlich
größere 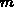 notwendig sein.
notwendig sein.
Neben der neugestarteten Form existiert auch eine
,,abgeschnittene`` (engl. truncated) Version.
In dieser Form werden bei der n-ten Iteration Basisvektoren,
die mehr als 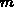 Iterationen zuvor konstruiert worden sind,
nicht mehr berücksichtigt und durch neue Basisvektoren
überschrieben. Im Gegensatz zur neugestarteten
Version ist die Monotonie dieser Iteration nicht
gewährleistet. Diese Version wurde im Rahmen
dieser Arbeit nicht verwendet.
Iterationen zuvor konstruiert worden sind,
nicht mehr berücksichtigt und durch neue Basisvektoren
überschrieben. Im Gegensatz zur neugestarteten
Version ist die Monotonie dieser Iteration nicht
gewährleistet. Diese Version wurde im Rahmen
dieser Arbeit nicht verwendet.
Ein gewisses Notationsproblem bei GMRES(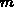 )
ist die Zählung der Iterationen. Inkrementiert
man den Iterationszähler nach der Berechnung eines
neuen Arnoldi-Vektors, so ist die Zahl der pro Iteration
durchzuführenden arithmetischen Operationen leicht vergleichbar
mit anderen iterativen Algorithmen. Allerdings ist
der Lösungsvektor nur alle
)
ist die Zählung der Iterationen. Inkrementiert
man den Iterationszähler nach der Berechnung eines
neuen Arnoldi-Vektors, so ist die Zahl der pro Iteration
durchzuführenden arithmetischen Operationen leicht vergleichbar
mit anderen iterativen Algorithmen. Allerdings ist
der Lösungsvektor nur alle 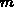 -Iterationen verfügbar.
Das Residuum kann hingegen auch während des Aufbaus der
Arnoldi-Vektoren ohne zusätzlichen Aufwand beobachtet werden,
wenn die QR-Faktoren zur Lösung des Hessenberg-Problems
kleinster Quadrate bei jedem Iterationsschritt mitgeschrieben werden.
-Iterationen verfügbar.
Das Residuum kann hingegen auch während des Aufbaus der
Arnoldi-Vektoren ohne zusätzlichen Aufwand beobachtet werden,
wenn die QR-Faktoren zur Lösung des Hessenberg-Problems
kleinster Quadrate bei jedem Iterationsschritt mitgeschrieben werden.



