1.4 Streumechanismen in unpolaren Halbleitern

Leitungselektronen in einem Halbleiter sind verschiedensten Wechselwirkungen ausgesetzt, die deren Beweglichkeit deutlich herabsetzen. In stark dotierten Halbleitern ist die Streuung an ionsierten Störstellen der domimante Streuprozeß. Neben der ionisierten Störstellenstreuung, die wir in Kapitel 3 ausführlich behandeln wollen, spielt die Phononenstreuung eine wichtige Rolle beim Transportverhalten von Elektronen im Kristall. Gitteratome schwingen bei endlicher Temperatur um ihre Ruhelage. Dadurch ist die räumliche Symmetrie des Gitters gestört, die die Ursache für die Streuung von Ladungsträgern in einem Kristall ist.

Der Zustand des ungestörten Systems $\left\vert\vec{k},c\right \gt$, das sich im Einelektronenzustand $\left\vert\vec{k}\right\gt$ und im Zustand des gesamten Kristalls $\left\vert c\right\gt$ befindet, wird als Produkt der Zustandsfunktion des einen Elektrons und der Zustandsfunktion des gesamten Kristalls zusammengesetzt,

$$\begin{eqnarray}\left\vert\vec{k},c\right\gt=\left\vert\vec{k}\right\gt\left\vert c\right\gt\; .\end{eqnarray}$$ (1.60)

Dann kann unter der Voraussetzung, daß der ungestörte Hamilton-Operator zeitunabhängig und die Störung gleichfalls zeitunabhängig ist oder nur eine periodische Zeitabhängigkeit aufweist [Mes90b], die Übergangswahrscheinlichkeit pro Zeiteinheit $P(\vec{k},c;\vec{k'},c')$ zwischen zwei Zuständen, die von einer kleinen Störung H_S hervorgerufen wird, in erster Ordnung mit der goldenen Regel von Fermi [Mes90a]

$$\begin{eqnarray}P(\vec{k},c;\vec{k'},c')= \frac{2\pi}{\hbar}\left\vert \left<\v... ...\delta\left[E_{n'}(\vec{k'})-E_n(\vec{k})\pm\Delta E(c',c)\right]\end{eqnarray}$$ (1.61)

berechnet werden, wobei die $\delta$-Funktion die Energieerhaltung angibt. Die Energiedifferenz des Kristalls wird dabei als $\Delta E(c',c)$bezeichnet. Im allgemeinen ist der Hamilton-Operator $H_S(\vec{r},\vec{y})$ eine Funktion der Raumkoordinaten des Elektrons $\vec{r}$ und der augenblicklichen Verschiebung der Ionenrümpfe aus deren Gleichgewichtslage $\vec{y}$. Es ist nun angebracht, die Fouriertransformierte des Hamilton-Operators bezüglich der Koordinate $\vec{r}$ des Elektrons zu bilden, da der Elektronenzustand als ebene Welle angesetzt wird und der Hamilton-Operator in einen Term, der nur auf das Kristallsystem wirkt, und einen Term, der nur auf das Elektron wirkt, aufgespaltet werden kann. Man erhält für das Matrixelement

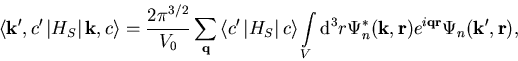$$\begin{eqnarray}\left< \vec{k'},c' \left\vert H_S\right\vert\vec{k},c\right\gt=... ..._n^*(\vec{k},\vec{r})e^{i\vec{q}\vec{r}}\Psi_n(\vec{k'},\vec{r}),\end{eqnarray}$$ (1.62)

wenn über das gesamte Volumen V des Materials integriert wird. Das Integral in (1.62) wird nun mit der Transformation $\vec{r'}'=\vec{r}-\vec{R}$ umgeformt. Der Vektor $\vec{R}$ führt zu einer Zelle im Raumgitter, $\vec{r'}'$ gibt die Lage des Elektrons innerhalb dieser Zelle an. Außerdem sei die Wellenfunktion auf die Anzahl der Gitterzellen N_g normiert. Damit ergibt sich mit dem Volumen der Einheitszelle im Raumgitter V_cell

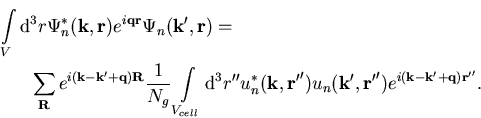$$\begin{eqnarray}\lefteqn{\int\limits_{V} {\mathrm d}^3 r\Psi_n^*(\vec{k},\vec{r... ...u_n(\vec{k'},\vec{r'}')e^{i(\vec{k}-\vec{k'}+\vec{q})\vec{r'}'}.\end{eqnarray}$$ (1.63)

Bei näherer Betrachtung zeigt sich, daß man die Summe aller Zellen im Kristall als

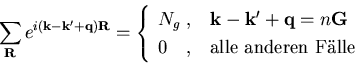$$\begin{eqnarray}\sum_{\vec{R}}e^{i(\vec{k}-\vec{k'}+\vec{q})\vec{R}}= \left\{\... ...c{G} \\ 0 & \mbox{alle anderen F\uml {a}lle}\end{array}\right.\end{eqnarray}$$ (1.64)

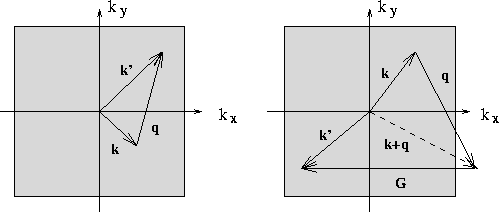
ausdrücken kann, wobei $\vec{G}$ ein Gittervektor des reziproken Gitters ist. Die Prozesse können nun in Normalprozeß, falls n gleich Null ist, oder als Umklappprozeß, falls n ungleich Null ist, unterteilt werden. Faßt man nun alle Beiträge zusammen, so kann man für die Übergangswahrscheinlichkeit folgendes Ergebnis

$$\begin{eqnarray}P(\vec{k},c;\vec{k'},c') = \frac{(2\pi)^4}{\hbar V_0^2}\left\ve... ...\delta\left[E_{n'}(\vec{k'})-E_n(\vec{k})\pm\Delta E(c',c)\right]\end{eqnarray}$$ (1.65)

anschreiben, wobei der Überlappungsfaktor als Integral

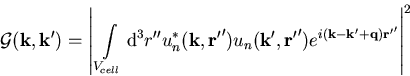$$\begin{eqnarray}{\cal G}(\vec{k},\vec{k'}) = \left\vert \,\int\limits_{V_{cell}... ...,\vec{r'}')e^{i(\vec{k}-\vec{k'}+\vec{q})\vec{r'}'}\right\vert^2\end{eqnarray}$$ (1.66)

definiert ist. Dieser Faktor wird, da in den meisten Fällen auch das Matrixelement $\left< c' \left\vert H_S\right\vert c\right\gt$ nicht genau bekannt ist, bei der Berechnung der Streuraten oft vernachlässigt, als konstant angesetzt oder aber in das Matrixelement einbezogen [JL89].
 

Der nächste Schritt, um die totale Streurate $\lambda(\vec{k})$ zu erhalten, besteht aus der Summation über alle Endzustände $\vec{k'}$. Unter der Annahme von kontinuierlichen Zuständen kann die Summation durch eine Integration ersetzt werden,

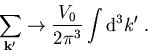$$\begin{eqnarray}\sum_{\vec{k'}} \rightarrow \frac{V_0}{2\pi^3}\int {\mathrm d}^3 k' \; .\end{eqnarray}$$ (1.67)

Man erhält damit für die differentielle Streurate

$$\begin{eqnarray}S(\vec{k'},\vec{k}) & = & \frac{V_0}{2\pi^3}P(\vec{k'},c';\vec{k},c)\end{eqnarray}$$ (1.68)

und für die totale Streurate

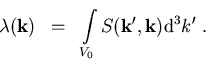$$\begin{eqnarray}\lambda(\vec{k}) & = & \int\limits_{V_0}S(\vec{k'},\vec{k}){\mathrm d}^3 k' \; .\end{eqnarray}$$ (1.69)

Eine weitere Auswertung der Streuprozesse hängt von den physikalischen Eigenschaften und von der verwendeten Bandstruktur für das jeweilige Material ab. Bei dieser Näherung erster Ordnung gilt die Energieerhaltung, und ferner hat die Wechselwirkung der Elektronen mit dem Kristall eine unendliche Lebensdauer. Eine rigorose Behandlung der Streuraten mit Hilfe von Green-Funktionen kann grundsätzlich durchgeführt werden [Joa75], doch speziell deren Lösung mittels iterativer Verfahren ist sehr aufwendig. Um den Zustand des Elektrons nach der Streuung zu ermitteln, ist es notwendig, die Winkelverteilung des betrachteten Streuprozesses zu kennen. Gibt es keine Winkelabhängigkeit, so wird der Stoß isotrop verlaufen, andernfalls muß der polare Winkel gemäß dieser Verteilung berechnet werden (vgl. Abschnitt 3.5).

 

• 1.4.1 Phononenstreuung
• 1.4.1.1 Akustische Deformationspotentialstreuung
• 1.4.1.2 Optische Zwischentalstreuung
• 1.4.2 Plasmonenstreuung