Next: 3.5 Zustand nach der Streuung Up: 3 Monte-Carlo-Methode Previous: 3.3 Mittelwertbildung
![]()
![]()
![]()
Next: 3.5
Zustand nach der Streuung Up: 3
Monte-Carlo-Methode Previous: 3.3
Mittelwertbildung
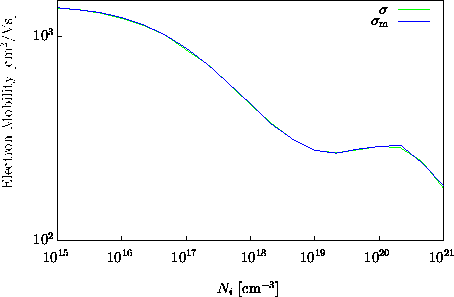 |
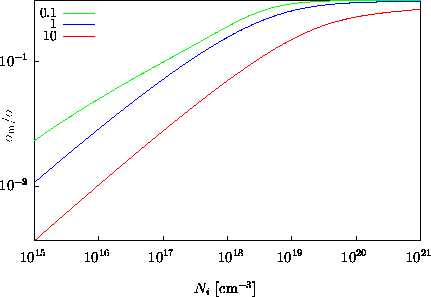
Streuprozesse wie die Streuung an ionisierten Störstellen liefern
besonders bei niedriger Dotierung kleine Streuwinkel, die die Beweglichkeit
kaum beeinflußen, jedoch oft über 90% der Streuungen ausmachen,
da auf Grund der langreichweitigen Coloumb-Wechselwirkung der Streuwirkungsquerschnitt
bei schwacher Abschirmung sehr groß wird (Abbildung 3.5).
Der scheinbare Widerspruch liegt darin, daß nicht der totale Streuwirkungsquerschnitt
(1.4), sondern der Impulswirkungsquerschnitt
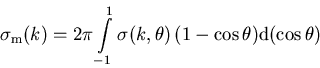 |
(3.24) |
die Beweglichkeit ![]() bestimmt.
bestimmt. ![]() ist also das Integral des differentiellen Wirkungsquerschnitts
ist also das Integral des differentiellen Wirkungsquerschnitts ![]() ,
gewichtet mit der Differenz aus dem Betrag der Gruppengeschwindigkeit und
deren x-Komponente. Um den Einfluß von
,
gewichtet mit der Differenz aus dem Betrag der Gruppengeschwindigkeit und
deren x-Komponente. Um den Einfluß von ![]() auf die Beweglichkeit zu verstehen, wollen wir vom Streuterm der Boltzmann-Transportgleichung
ausgehen, der im nicht-entarteten Fall lautet
auf die Beweglichkeit zu verstehen, wollen wir vom Streuterm der Boltzmann-Transportgleichung
ausgehen, der im nicht-entarteten Fall lautet
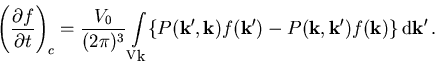 |
(3.25) |
Wenn man nun (3.25) mit ![]() multipliziert und über alle
multipliziert und über alle ![]() integriert, erhält man die mittlere Impulsverlustrate infolge von
Streuprozessen:
integriert, erhält man die mittlere Impulsverlustrate infolge von
Streuprozessen:
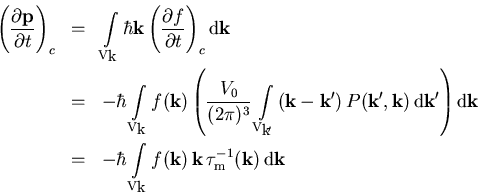 |
(3.26) |
 |
Der Übergang in (3.26) setzt voraus,
daß P nicht vom Azimutwinkel ![]() ,
sondern nur vom Streuwinkel
,
sondern nur vom Streuwinkel ![]() abhängt, also ein zylindersymmetrisches Problem vorliegt. Für
ein zentralsymmetrisches Potential ist diese Annahme erfüllt. Aus
(3.26) sieht man nun, warum
abhängt, also ein zylindersymmetrisches Problem vorliegt. Für
ein zentralsymmetrisches Potential ist diese Annahme erfüllt. Aus
(3.26) sieht man nun, warum ![]() im Fall von stark anisotropen Streuprozessen um Größenordnungen
kleiner sein kann. Die Impulsrelaxationszeit
im Fall von stark anisotropen Streuprozessen um Größenordnungen
kleiner sein kann. Die Impulsrelaxationszeit ![]() ist nämlich definiert als
ist nämlich definiert als
| |
(3.27) |
Nun läßt sich die Beweglichkeit nach [BKBM+87,LT92]
definieren als
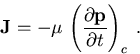 |
(3.28) |
In dieser allgemeinen Definition ist ![]() ein Tensor, da infolge anisotroper Bandstruktur und nicht-symmetrischer
Verteilungsfunktion die Stromdichte
ein Tensor, da infolge anisotroper Bandstruktur und nicht-symmetrischer
Verteilungsfunktion die Stromdichte ![]() und die vektorwertige Impulsverlustrate im allgemeinen nicht kollinear
sind. Die Elektronenstromdichte ist definiert als
und die vektorwertige Impulsverlustrate im allgemeinen nicht kollinear
sind. Die Elektronenstromdichte ist definiert als
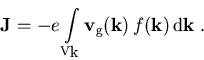 |
(3.29) |
 |
Eine skalare Beweglichkeit erhalten wir nun durch Betragsbildung von (3.29)
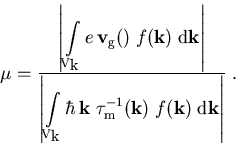 |
(3.30) |
Aus (3.30) erkennt man, daß
für die Beweglichkeit der Impulswirkungsquerschnitt maßgeblich
ist und nicht der Stoßwirkungsquerschitt, der in der Monte-Carlo-Methode
zur Berechnung der totalen Streurate benötigt wird. Das ist auch der
Grund, warum bei niedriger Dotierung trotz dominierender Störstellenstreuung
die Beweglichkeit von vergleichsweise wenigen Phononenstreuprozessen bestimmt
wird. Man kann nun zeigen, daß es zur Berechnung der Niederfeldbeweglichkeit
unter bestimmtem Voraussetzungen irrelevant ist, ob man die totale Streurate
über den Stoßquerschnitt ![]() berechnet oder aber
berechnet oder aber ![]() zu Hilfe nimmt und eine isotrope Winkelverteilung nach der Streuung annimmt.
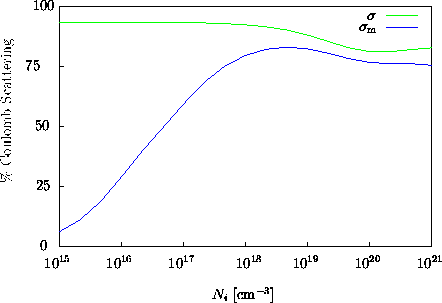
Neben der Gültigkeit der goldenen Regel von Fermi muß vorausgesetzt
werden, daß die Verteilungsfunktion als Reihe in Legendre-Polynome
höchstens erster Ordnung darstellbar ist. Da Glieder höherer
Ordnung in
zu Hilfe nimmt und eine isotrope Winkelverteilung nach der Streuung annimmt.
Neben der Gültigkeit der goldenen Regel von Fermi muß vorausgesetzt
werden, daß die Verteilungsfunktion als Reihe in Legendre-Polynome
höchstens erster Ordnung darstellbar ist. Da Glieder höherer
Ordnung in ![]() für die Ohmsche Beweglichkeit keine Rolle spielen, ist diese Approximation
in allen praktischen Anwendungen vollkommen ausreichend (Abbildung 3.6).
Durch die Einführung eines solchen isotropen Streuprozesses erzielt
man zwei Verbesserungen. Einerseits vermindert sich die Zahl der Kleinwinkelstreuungen
um Größenordnungen, und andererseits fällt die oft nur
numerisch mögliche Berechnung der anisotropen Winkelverteilung des
Elektrons nach der Streuung weg [Kos97]
(Abbildung 3.7). Das oft zitierte und weit verbreitete
Modell von Ridley [Rid77], daß den
Wirkungsquerschnitt exponentiell mit einem eher willkürlichen Parameter
wichtet, um kleine Streuwinkel zu unterbinden, sollte vermieden werden,
da es die Beweglichkeit willkürlich verändert.
für die Ohmsche Beweglichkeit keine Rolle spielen, ist diese Approximation
in allen praktischen Anwendungen vollkommen ausreichend (Abbildung 3.6).
Durch die Einführung eines solchen isotropen Streuprozesses erzielt
man zwei Verbesserungen. Einerseits vermindert sich die Zahl der Kleinwinkelstreuungen
um Größenordnungen, und andererseits fällt die oft nur
numerisch mögliche Berechnung der anisotropen Winkelverteilung des
Elektrons nach der Streuung weg [Kos97]
(Abbildung 3.7). Das oft zitierte und weit verbreitete
Modell von Ridley [Rid77], daß den
Wirkungsquerschnitt exponentiell mit einem eher willkürlichen Parameter
wichtet, um kleine Streuwinkel zu unterbinden, sollte vermieden werden,
da es die Beweglichkeit willkürlich verändert.