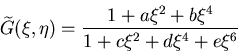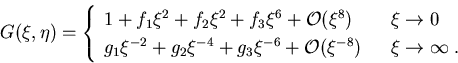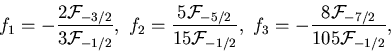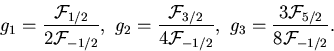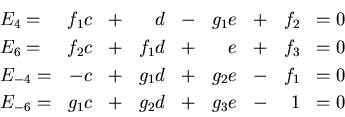

Next: 4.1.2 Simultane Streuung an zwei Störstellen
Up: 4.1 Majoritätselektronen
Previous: 4.1 Majoritätselektronen
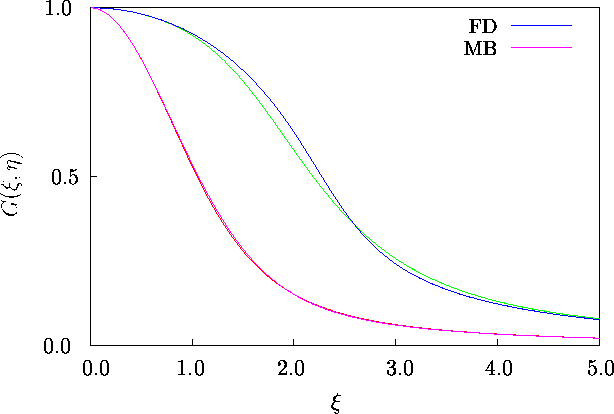
Abbildung 4.1:
Die exakte Abschirmfunktion 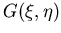 im nicht-entarteten (MB) und entarteten Fall für
im nicht-entarteten (MB) und entarteten Fall für 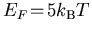 . Die rationale Approximation ist im
ersten Fall (rosa) sehr genau für alle
. Die rationale Approximation ist im
ersten Fall (rosa) sehr genau für alle 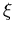 . Im entarteten Fall (grün) ist die Übereinstimmung für
. Im entarteten Fall (grün) ist die Übereinstimmung für 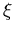 kleiner eins und für
kleiner eins und für 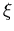 größer drei sehr gut. Man kann zeigen,
daß das mittlere
größer drei sehr gut. Man kann zeigen,
daß das mittlere 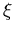 für den Großteil aller Coulomb-Streuprozesse kleiner, ja sehr oft viel kleiner als eins ist (Anhang F). Das bedeutet, daß eine Ungenauigkeit für
für den Großteil aller Coulomb-Streuprozesse kleiner, ja sehr oft viel kleiner als eins ist (Anhang F). Das bedeutet, daß eine Ungenauigkeit für 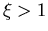 praktisch keine Auswirkung auf die Beweglichkeit hat.
praktisch keine Auswirkung auf die Beweglichkeit hat.
 |
Die Abschirmfunktion 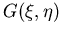 (4.1) beschreibt das dynamische Verhalten der Leitungselektronen bei der Streuung eines Elektrons an einer
ionisierten Störstelle. Aufgrund der abstoßenden Ladungen zwischen herannahendem Elektron und dem restlichen Elektronengas kommt es zu einer Polarisation, die
die Abschirmung der Störstelle impulsabhängig macht. Bei nieriger Dotierung überwiegt die
Kleinwinkelstreuung, sodaß
(4.1) beschreibt das dynamische Verhalten der Leitungselektronen bei der Streuung eines Elektrons an einer
ionisierten Störstelle. Aufgrund der abstoßenden Ladungen zwischen herannahendem Elektron und dem restlichen Elektronengas kommt es zu einer Polarisation, die
die Abschirmung der Störstelle impulsabhängig macht. Bei nieriger Dotierung überwiegt die
Kleinwinkelstreuung, sodaß 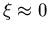 wird und
wird und 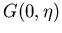 gegen Eins strebt. Das oft zitierte BH-Modell geht von dieser Annahme aus. Mit zunehmender
Dotierung nehmen die Streuwinkel zu, sodaß die q-Abhängigkeit
von G nicht vernachlässigbar ist. Wir wollen G durch eine
rationale Funktion der Form
gegen Eins strebt. Das oft zitierte BH-Modell geht von dieser Annahme aus. Mit zunehmender
Dotierung nehmen die Streuwinkel zu, sodaß die q-Abhängigkeit
von G nicht vernachlässigbar ist. Wir wollen G durch eine
rationale Funktion der Form
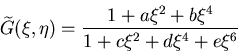 |
(4.1) |
annähern. Der Grad vom Nennerpolynom muß um 2 höher als der des
Zählerpolynoms sein, um das korrekte Verhalten im Unendlichen wiederzugeben.
Die Taylorreihen von G, entwickelt um Null und im Unendlichen, ergeben
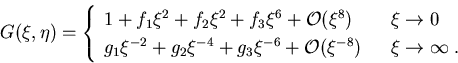 |
(4.2) |
Dabei lauten die Koeffizienten
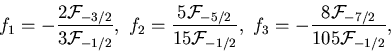 |
(4.3) |
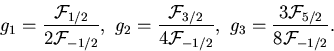 |
(4.4) |
Durch Koeffizientenvergleich von G und 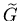 erhalten wir ein
lineares Gleichungssystem für die Unbekannten (a,b,c,d,e).
Da wir unendliche Reihen vergleichen, bleibt noch zu entscheiden,
bis zu welcher Ordnung diese miteinander übereinstimmen sollen. Es wird ein
Koeffizientenvergleich der Taylorreihen von G und
erhalten wir ein
lineares Gleichungssystem für die Unbekannten (a,b,c,d,e).
Da wir unendliche Reihen vergleichen, bleibt noch zu entscheiden,
bis zu welcher Ordnung diese miteinander übereinstimmen sollen. Es wird ein
Koeffizientenvergleich der Taylorreihen von G und 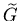 vorgenommem. Die Gleichheit der Koeffizienten von
vorgenommem. Die Gleichheit der Koeffizienten von 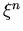 ergibt die Gleichung En.
Damit die Reihen in den
Potenzen
ergibt die Gleichung En.
Damit die Reihen in den
Potenzen 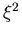 und
und 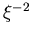 übereinstimmen, erhalten wir die Gleichungen
a=c+f1 und b=g1 e. Damit reduzieren wir den Rang des Gleichungssystems auf drei und erhalten
übereinstimmen, erhalten wir die Gleichungen
a=c+f1 und b=g1 e. Damit reduzieren wir den Rang des Gleichungssystems auf drei und erhalten
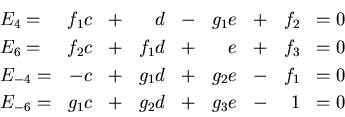 |
(4.5) |
E4 und E-4 können gleichzeitig gelöst werden, wodurch sich eine
exakte Übereinstimmung in den Potenzen 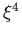 and
and 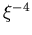 ergibt.
Da die Gleichungen E6 und E-6 nicht gleichzeitig gelöst werden können, wurde eine Linearkombination
ergibt.
Da die Gleichungen E6 und E-6 nicht gleichzeitig gelöst werden können, wurde eine Linearkombination
gewählt. Es kann gezeigt werden, daß der optimale Wert des
Parameters u
als Funktion der reduzierten Fermi-Energie gleich 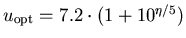 ist [KKG97].
ist [KKG97].
Abbildung 4.2:
Einfluß der dispersiven Abschirmung (DS) auf die Elektronenbeweglichkeit als Funktion
der Dotierung bei 300 K. Im Vergleich dazu das oft verwendete BH Modell, in dem
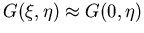 gesetzt wird. Die experimentellen Daten sind [MSS83]
entnommen.
gesetzt wird. Die experimentellen Daten sind [MSS83]
entnommen.
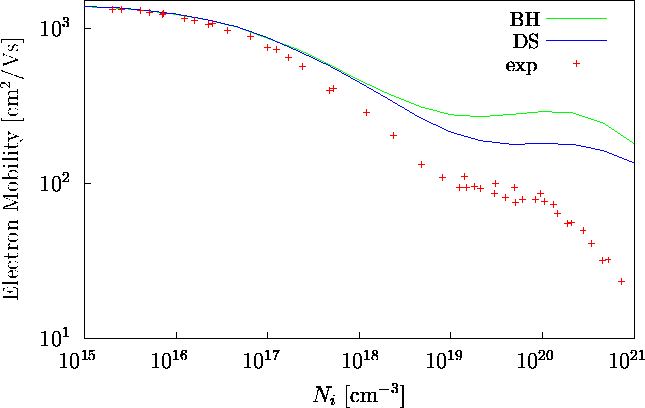 |
Aus Abbildung 4.2 erkennt man einerseits, daß die q-Abhängigkeit der dielektrischen Abschirmung ab 1018 cm-3 wichtig wird, während sie andererseits jenseits 1021 cm-3 wieder verschwindet. Der Grund dafür ist, daß bei hoher
Entartung 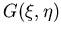 praktisch von
praktisch von 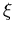 unabhängig wird. Das ist
auch der Grund, warum die dispersive Abschirmung bei Verbindungshalbleitern, wie GaA und InP eine untergeordnete Rolle spielt [CF88].
unabhängig wird. Das ist
auch der Grund, warum die dispersive Abschirmung bei Verbindungshalbleitern, wie GaA und InP eine untergeordnete Rolle spielt [CF88].


Next: 4.1.2 Simultane Streuung an zwei Störstellen
Up: 4.1 Majoritätselektronen
Previous: 4.1 Majoritätselektronen
Kaiblinger-Grujin Goran
1997-12-06