Next: 4.1.4 Pauli-Verbot Up: 4.1 Majoritätselektronen Previous: 4.1.2 Simultane Streuung an zwei Störstellen
![]()
![]()
![]()
Next: 4.1.4
Pauli-Verbot Up: 4.1
Majoritätselektronen Previous: 4.1.2
Simultane Streuung an zwei Störstellen
 |
Das BH Modell verwendet die Born-Näherung erster Ordnung, sodaß
man zwischen Minoritäten und Majoritäten nicht unterscheiden
kann![]() .
Andererseits gibt die Born-Näherung erster Ordnung für verschwindende
Abschirmung den exakten Wirkungsquerschnitt [Joa75].
Will man höhere Ordnungen berücksichtigen, muß man erkennen,
daß schon die Streuamplitude zweiter Ordnung (1.46)
für
.
Andererseits gibt die Born-Näherung erster Ordnung für verschwindende
Abschirmung den exakten Wirkungsquerschnitt [Joa75].
Will man höhere Ordnungen berücksichtigen, muß man erkennen,
daß schon die Streuamplitude zweiter Ordnung (1.46)
für ![]() divergiert. Wir können diese Divergenz jedoch umgehen, indem wir die
Streuamplitude nach Schwinger (1.48) benutzen,
um eine Korrektur
divergiert. Wir können diese Divergenz jedoch umgehen, indem wir die
Streuamplitude nach Schwinger (1.48) benutzen,
um eine Korrektur ![]() zu
zu ![]() zu berechnen [Sch47]. Aus Konsistenzgründen
vernachlässigen wir die dispersive Abschirmung und die Paarstreuung
und benutzen (1.46). Durch geeignete Substitution
konnten wir in Abschnitt (1.3.3) eine
Reihenentwicklung (1.55) für die Streuamplitude
nach Schwinger erhalten, die für jede Dotierung innerhalb des Konvergenzradius
bleibt. Für
zu berechnen [Sch47]. Aus Konsistenzgründen
vernachlässigen wir die dispersive Abschirmung und die Paarstreuung
und benutzen (1.46). Durch geeignete Substitution
konnten wir in Abschnitt (1.3.3) eine
Reihenentwicklung (1.55) für die Streuamplitude
nach Schwinger erhalten, die für jede Dotierung innerhalb des Konvergenzradius
bleibt. Für ![]() erhalten wir damit
erhalten wir damit
| |
(4.7) |
wobei a1 durch (1.56)
definiert ist. Man erkennt aus (1.56),
daß wir sogar in nullter Ordnung der zweiten Born-Amplitude eine
Korrektur erhalten, die Minoritäten von Majoritäten über
U0 unterscheidet. Da a1 von q
unabhängig ist, ändert sich die Winkelverteilung nicht, sodaß
wir dieselbe Begrenzungsfunktion für (4.7)
benutzen können wie für ![]() .
Mit Hilfe der Verwerfungsmethode (siehe Abschnitt (3.5))
läßt sich dann der Streuprozeß auswählen. Wir können
nun die Divergenz der zweiten Born-Näherung unterbinden, indem wir
fordern, daß s0 nicht negativ werden darf. Ein
negatives s0 würde
.
Mit Hilfe der Verwerfungsmethode (siehe Abschnitt (3.5))
läßt sich dann der Streuprozeß auswählen. Wir können
nun die Divergenz der zweiten Born-Näherung unterbinden, indem wir
fordern, daß s0 nicht negativ werden darf. Ein
negatives s0 würde ![]() reduzieren und sogar exakt kompensieren, da s0 für
verschwindende Abschirmung gegen Eins strebt. Da aber
reduzieren und sogar exakt kompensieren, da s0 für
verschwindende Abschirmung gegen Eins strebt. Da aber ![]() für verschwindende Abschirmung den exakten Wirkungsquerschnitt darstellt,
ist es physikalisch sinnvoll, negative Werte für s0
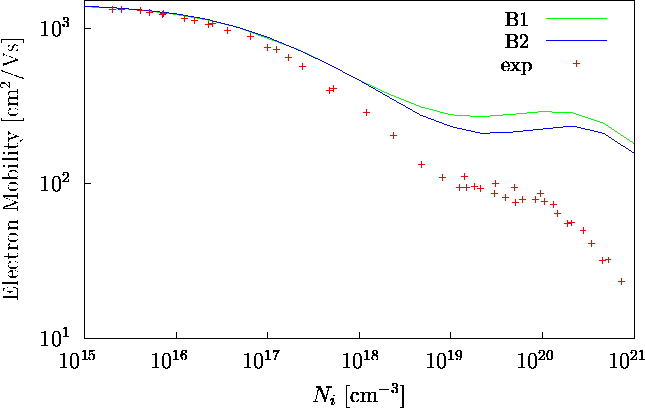
auszuschließen. In Abbildung 4.4 ist der Einfluß
der zweiten Born-Korrektur nullter Ordnung auf die Beweglichkeit von Majoritätselektronen
zu sehen. Diese Korrektur kann als untere Schranke für den Wirkungsquerschnitt
zweiter Ordnung angesehen werden, da alle Glieder höherer Ordnung
positiv sind. Für die Beweglichkeit bedeutet das, daß Korrekturen
der zweiten Born-Näherung eine obere Schranke für die Beweglichkeit
bedeuten.
für verschwindende Abschirmung den exakten Wirkungsquerschnitt darstellt,
ist es physikalisch sinnvoll, negative Werte für s0
auszuschließen. In Abbildung 4.4 ist der Einfluß
der zweiten Born-Korrektur nullter Ordnung auf die Beweglichkeit von Majoritätselektronen
zu sehen. Diese Korrektur kann als untere Schranke für den Wirkungsquerschnitt
zweiter Ordnung angesehen werden, da alle Glieder höherer Ordnung
positiv sind. Für die Beweglichkeit bedeutet das, daß Korrekturen
der zweiten Born-Näherung eine obere Schranke für die Beweglichkeit
bedeuten.