Next: 5.1 Beweglichkeit von Majoritätselektronen Up: Dissertation G. Kaiblinger-Grujin Previous: 4.2 Minoritätselektronen
![]()
![]()
![]()
Next: 5.1
Beweglichkeit von Majoritätselektronen Up: Dissertation
G. Kaiblinger-Grujin Previous: 4.2
Minoritätselektronen
Da die Niederfeldbeweglichkeit einen wichtigen Parameter zur Analyse und zum Entwurf von Halbleiterbauelementen darstellt, sind genaue Beweglichkeitsmodelle von großer Wichtigkeit. Die ohmsche Beweglichkeit in dotierten Halbleitern ist eine Funktion der Störstellenkonzentration und der Temperatur. Experimentelle Untersuchungen scheinen auf ein unterschiedliches Transporterhalten von Elektronen in n- und p-dotiertem Silizium hinzuweisen. In einem n-Gebiet sind die Elektronen aufgrund der ionisierten Donatoratome einem anziehenden Streupotential ausgesetzt, während hingegen in einem p-Gebiet die ionisierten Akzeptoratome ein abstoßendes Potential erzeugen, an dem die Elektronen gestreut werden. Da üblicherweise im Bereich der Bauelementsimulation praktisch nur mit der ersten Born-Näherung (unter Annahme einer punktförmigen Störstelle, siehe Abschnitt 2.4) gerechnet wird und in dieser der Streuquerschnitt nicht vom Vorzeichen der der Ladung einer ionisiserten Störstelle abhängt, blieb dieses unterschiedliche Verhalten bei der Modellierung oft unbeachtet. Natürlich muß man zugeben, daß dieses Phänomen erst bei höherer Dotierung eine Rolle spielt. Da in heutigen Bipolartransistoren p-Bereiche mit einer Störstellenkonzentration von 1019 cm-3 keine Seltenheit sind, müssen moderne Bauelementsimulatoren zwischen Majoritäts- und Minoritätselektronen unterscheiden. Denn bei 300 K ist in diesem Dotierungsbereich die Beweglichkeit von Minoritätselektronen mehr als doppelt so hoch als die Beweglichkeit von Majoritätselektronen [SKS86,LN93].
Experimente haben gezeigt, daß die Beweglichkeit der Elektronen
in Silizium vom Donatortyp abhängt. Der Unterschied in der Beweglichkeit zwischen
P- und As-dotiertem Si kann bis zu 32% bei 300 K betragen [MSS83].
Ein in [MSS83] vorgeschlagenes empirisches
Modell![]() ,
welches zwischen P- und As-dotiertem Si unterscheidet, findet des öfteren
in kommerziellen Simulatoren Verwendung.
,
welches zwischen P- und As-dotiertem Si unterscheidet, findet des öfteren
in kommerziellen Simulatoren Verwendung.
Nach wie vor verwenden viele Beweglichkeitsmodelle
[BO75,AHR82,
MBCR93]
als Basisformel jene von Caughey und Thomas [CT67],
die folgende Form hat:
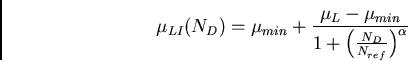 |
(5.1) |
![]() bezeichnet die Gitterbeweglichkeit, die durch die Phononstreuung begrenzt
wird.
bezeichnet die Gitterbeweglichkeit, die durch die Phononstreuung begrenzt
wird. ![]() ist jene Beweglichkeit, die sich durch die zusätzliche Streuung an
ionisierten Störstellen ergibt. (5.1)
reproduziert die Beweglichkeit bis
ist jene Beweglichkeit, die sich durch die zusätzliche Streuung an
ionisierten Störstellen ergibt. (5.1)
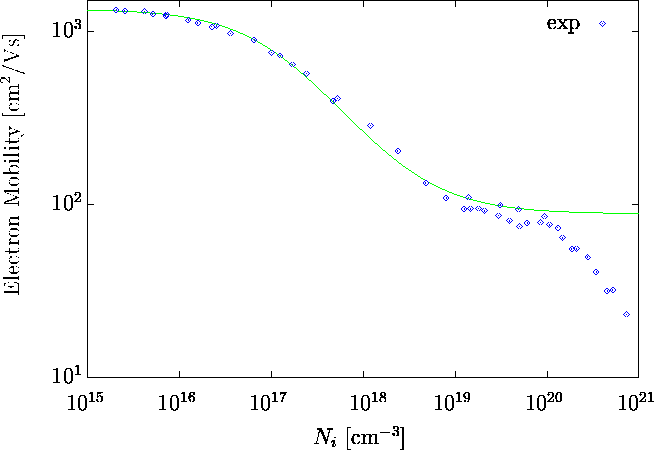
reproduziert die Beweglichkeit bis ![]() cm-3 ziemlich gut (Abb. 5.1).
Eine Zusammenfassung verschiedener Parametersätze für (5.1)
findet sich in [Sel84]. Da eine Funktion
der Form (5.1) jedoch kein lokales Minimum
besitzt, sondern monoton fällt, kann die Beweglichkeit jenseits von
1020 cm-3 auch qualitativ nicht wiedergegeben werden.
Theoretische Überlegungen sagen ein lokales Minimum voraus, daß
durch das Pauli-Verbot und durch das Verschwinden der Elektron-Plasmon Streuung
zustandekommt (Abb.1.2 und Abb.4.5).
Bei tiefen Temperaturen, wo dieses Minimum infolge stärkerer Entartung
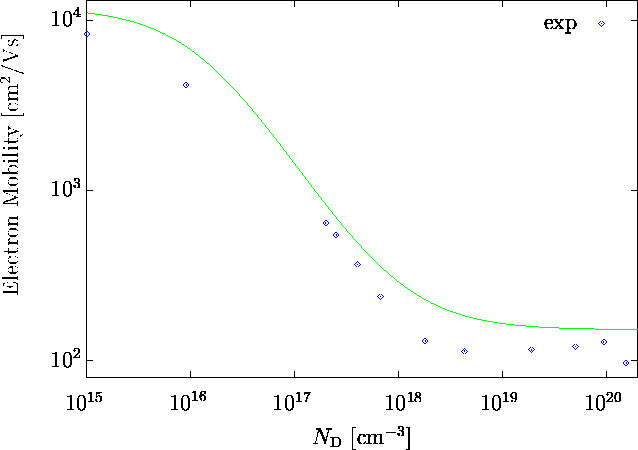
ausgeprägter ist, konnten Experimente bei 100 K [Swi87]
ein lokales Minimum bestätigen (Abb. 5.2).
Es soll jedoch nicht unerwähnt bleiben, daß sogar in leicht
dotiertem Silizium die Experimente zum Teil stark voneinander abweichen,
sodaß es schwierig ist, auch nur die Phononenbeweglichkeit eindeutig
festzustellen
[NBL73,BO75,LT77].
Experimente [Swi87] zeigen jedoch klar,
daß mit abnehmender Temperatur die Beweglichkeit eine Sättigung
erfährt, deren Ursache nicht ganz geklärt ist. Entweder gewinnt
die Streuung an neutralen Störstellen an Bedeutung, wobei keine zufriedenstellende
Theorie dafür existiert
cm-3 ziemlich gut (Abb. 5.1).
Eine Zusammenfassung verschiedener Parametersätze für (5.1)
findet sich in [Sel84]. Da eine Funktion
der Form (5.1) jedoch kein lokales Minimum
besitzt, sondern monoton fällt, kann die Beweglichkeit jenseits von
1020 cm-3 auch qualitativ nicht wiedergegeben werden.
Theoretische Überlegungen sagen ein lokales Minimum voraus, daß
durch das Pauli-Verbot und durch das Verschwinden der Elektron-Plasmon Streuung
zustandekommt (Abb.1.2 und Abb.4.5).
Bei tiefen Temperaturen, wo dieses Minimum infolge stärkerer Entartung
ausgeprägter ist, konnten Experimente bei 100 K [Swi87]
ein lokales Minimum bestätigen (Abb. 5.2).
Es soll jedoch nicht unerwähnt bleiben, daß sogar in leicht
dotiertem Silizium die Experimente zum Teil stark voneinander abweichen,
sodaß es schwierig ist, auch nur die Phononenbeweglichkeit eindeutig
festzustellen
[NBL73,BO75,LT77].
Experimente [Swi87] zeigen jedoch klar,
daß mit abnehmender Temperatur die Beweglichkeit eine Sättigung
erfährt, deren Ursache nicht ganz geklärt ist. Entweder gewinnt
die Streuung an neutralen Störstellen an Bedeutung, wobei keine zufriedenstellende
Theorie dafür existiert![]() ,
oder die Phononenbeweglichkeit folgt keinem einfachen Potenzgesetz. Letztere
Möglichkeit ist sehr wahrscheinlich, da im Grenzwert
,
oder die Phononenbeweglichkeit folgt keinem einfachen Potenzgesetz. Letztere
Möglichkeit ist sehr wahrscheinlich, da im Grenzwert ![]() die Phononenbeweglichkeit gegen Unendlich ginge und damit (5.1)
divergieren würde. Aus diesem Grunde habe ich
die Phononenbeweglichkeit gegen Unendlich ginge und damit (5.1)
divergieren würde. Aus diesem Grunde habe ich ![]() mit einer verschobenen Exponentialfunktion modelliert, die für verschwindende
Temperaturen gegen einen Grenzwert strebt ((5.3)
, Abbildung G.4.)
mit einer verschobenen Exponentialfunktion modelliert, die für verschwindende
Temperaturen gegen einen Grenzwert strebt ((5.3)
, Abbildung G.4.)
 |
Um die Beweglichkeit jenseits von 1020 cm-3 zu modellieren,
kann man zu (5.1) einen zweiten rationalen
Term addieren [MSS83]. Bei der Simulation
von Bipolartransistoren wird es notwendig, Majoritäts- und Minoritätsladungsträgerbeweglichkeiten
zu unterscheiden. Experimente lassen vermuten, daß bei tiefen Temperaturen
![]() um
mehr als eine Größenordnung größer ist als die
Beweglichkeit der Majoritätselektronen
In diesem Zusammenhang erwähnenswert ist das Beweglichkeitsmodell
von Klaassen [Kla92a,Kla92b],
welches ein mit physikalisch motivierten Ansätzen versehenes empirisches
Modell darstellt. Er unterscheidet in seinem Modell zwischen Majoritäts-
und Minoritätsladungsträgern, indem er zur ersten Born-Näherung
eine Korrekturfunktion multipliziert, die er durch Streuphasenrechnungen
erhält. Zwischen verschiedenen Dopanden eines Typs kann das Modell
jedoch nicht unterscheiden. Außerdem ist der gültige Temperaturbereich
nur [200,500] K, wobei die Übereinstimmung mit dem Experiment
oft nur für T>250 K akzeptabel ist. Außerdem wurden
in [Kla92a,Kla92b]
die Beweglichkeiten nur innerhalb des kleinen Dotierungsbereichs
um
mehr als eine Größenordnung größer ist als die
Beweglichkeit der Majoritätselektronen
In diesem Zusammenhang erwähnenswert ist das Beweglichkeitsmodell
von Klaassen [Kla92a,Kla92b],
welches ein mit physikalisch motivierten Ansätzen versehenes empirisches
Modell darstellt. Er unterscheidet in seinem Modell zwischen Majoritäts-
und Minoritätsladungsträgern, indem er zur ersten Born-Näherung
eine Korrekturfunktion multipliziert, die er durch Streuphasenrechnungen
erhält. Zwischen verschiedenen Dopanden eines Typs kann das Modell
jedoch nicht unterscheiden. Außerdem ist der gültige Temperaturbereich
nur [200,500] K, wobei die Übereinstimmung mit dem Experiment
oft nur für T>250 K akzeptabel ist. Außerdem wurden
in [Kla92a,Kla92b]
die Beweglichkeiten nur innerhalb des kleinen Dotierungsbereichs ![]() cm-3 mit experimentellen Daten verglichen. Es sollte auch erwähnt
werden, daß das vorausgesagte Temperaturverhalten nicht mit dem Experiment
in Einklang ist, wobei man zugeben muß, daß die Experimente
selbst zum Teil erheblich voneinander abweichen
[Dzi79,
Neu85,SKS86,
SKS88,LN93].
Der Grund ist, daß
cm-3 mit experimentellen Daten verglichen. Es sollte auch erwähnt
werden, daß das vorausgesagte Temperaturverhalten nicht mit dem Experiment
in Einklang ist, wobei man zugeben muß, daß die Experimente
selbst zum Teil erheblich voneinander abweichen
[Dzi79,
Neu85,SKS86,
SKS88,LN93].
Der Grund ist, daß
![]() nicht direkt gemessen wird, sondern über die Diffusivität und
über die Diffusionslänge nach der Einstein-Relation berechnet
wird. Dabei muß man ein Annahme über die temperatur- und konzentrationsabhängige
Lebenszeit der Minoritätselektronen treffen (Abschnitt 4.2).
nicht direkt gemessen wird, sondern über die Diffusivität und
über die Diffusionslänge nach der Einstein-Relation berechnet
wird. Dabei muß man ein Annahme über die temperatur- und konzentrationsabhängige
Lebenszeit der Minoritätselektronen treffen (Abschnitt 4.2).
 |