D Thomas-Fermi-Abschirmlänge

  Eine ionisierte Störstelle induziert eine räumlich inhomogene Ladung

$$\rho (r) = e\, \left[ n(r) -n_{0}\right] = e \,N_{C} \left[ ... ... \right) - {\cal F}_{\frac{1}{2}}\left(\eta \right) \right] ,$$ (D.1)

die über die Poisson-Gleichung

$$\Delta V (r) = - \frac{\rho (r)}{\epsilon_{0}\epsilon_{\mathrm{sc}}}$$ (D.2)

gekoppelt ist. n₀ bezeichnet die homogene Ladungsdichte ohne Beisein einer Störung. Durch Entwicklung der induzierten Ladung in eine Potenzreihe erster Ordnung nach der Störung V(r) unter Zuhilfenahme von ${\cal F}_{j}'(\eta) ={\cal F}_{j-1}(\eta)$ erhalten wir schließlich [Din55,Man56]

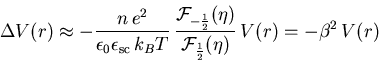$$\Delta V (r) \approx - \frac{n\,e^2}{\epsilon_{0}\epsilon_{\... ...a) }{{\cal F}_{\frac{1}{2}}(\eta) }\,V (r)=-\beta^{2}\, V (r)$$ (D.3)

Die Lösung dieser Differentialgleichung, die im Ursprung in die Lösung für das ungeschirmte Coulomb-Potenial übergehen und im Unendlichen verschwinden soll, ist das abgeschirmtes Coulomb-Potential

$$V(r) = -\frac{Q\,e}{4\pi\epsilon_{0}\epsilon_{\mathrm{sc}}r} {\mathrm{} e}^{-\beta r} \; ,$$ (D.4)

das auch als Thomas-Fermi-Potential bekannt ist.