E Friedel-Summenregel

  Die Friedel-Summenregel folgt aus der Ladungserhaltung in einem Festkörper. Bringt man eine ionisierte Störstelle in einem Halbleiter ein, so versuchen freie Ladungsträger diese elektrische Störung abzuschirmen und dadurch einen Ladungsausgleich zu bewirken. Benutzt man die erste Born-Näherung (1.16),

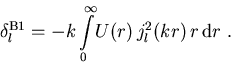$$\sin\delta_{l}=-\int_{0}^{\infty} kr j_{l} (kr) U(r) \, u_{l}(r) {\mathrm d} r$$ (E.1)

für die Streuphasen, so kann man folgende Bedingung zwischen der Ladung Q einer Störstelle und dem Störpotential V aufstellen [Ste67]

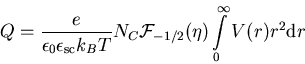$$Q = \frac{e}{\epsilon_{0}\epsilon_{\mathrm{sc}}k_B T} N_C {\cal F}_{-1/2}(\eta) \int\limits_0^\inftyV (r) r^2 {\mathrm d}r$$ (E.2)

wobei N_C die effektive Zustandsdichte des Leitungsbandes ist. Korrekturen zu (E.2), die die zweite Born-Näherung benutzen, finden sich in [PL89]. In (E.2) wurde vorausgesetzt, daß der Halbleiter sphärische Energieflächen hat und das Streupotential sphärisch symmetrisch ist und schneller als r^-1 gegen Null abfällt. Die Friedel-Summenregel gilt, solange die Streuzentren nicht miteinander wechselwirken und die Wellenlänge des Elektrons kleiner ist als der mittlere Abstand benachbarter Störstellen [KFH76,BSM92]. Daher wollen wir im folgenden Interferenzeffekte außer acht lassen. Wir können nach (2.24) das Potential einer Störstelle schreiben als

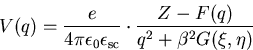$$V(q) = \frac{e}{4\pi\epsilon_0\epsilon_{\mathrm{sc}}}\cdot\frac{Z-F(q)}{q^2+\beta^2 G(\xi,\eta)}$$ (E.3)

Da wir G als rationale Funktion dargestellt haben, ist auch V eine rationale Funktion, die wir in eine Summe von rationalen Funktionen nach q² zerlegen können.

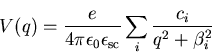$$V(q)=\frac{e}{4\pi\epsilon_0\epsilon_{\mathrm{sc}}}\sum\limits_i \frac{c_i}{q^2+\beta_i^2}$$ (E.4)

Die $\beta_i^2$ sind die Wurzeln des Nennerpolynoms von V. Wenn man nun (E.3) und (E.4) für q=0 auswertet, erhält man für c_i und $\beta_i^2$ folgende Beziehung:

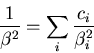$$\frac{1}{\beta^2} = \sum_i \frac{c_i}{\beta_i^2}$$ (E.5)

Einsetzen von (E.5) in (E.3) ergibt in Ortsraum eine Summe von abgeschirmten Coulomb-Potentialen

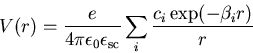$$V(r)=\frac{e}{4\pi\epsilon_0\epsilon_{\mathrm{sc}}}\sum\limits_i\frac{c_i \exp(-\beta_i r)}{r}$$ (E.6)

Einsetzen von (E.6) in (E.2) mit anschließender Integration liefert

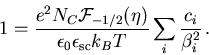$$1=\frac{e^2 N_C {\cal F}_{-1/2}(\eta)}{\epsilon_0\epsilon_{\mathrm{sc}} k_B T}\sum\limits_i \frac{c_i}{\beta_i^2}\,.$$ (E.7)

Berücksichtigt man nun (D.3) und die Bedingung (E.5), so kann man leicht zeigen, daß die Friedel-Summenregel erfüllt ist. Bemerkenswert ist, daß (E.5) eine Bedingung für $\beta$ oder $G(0,\eta)$ angibt, jedoch die q-Abhängigkeit von G keinerlei Bedingung unterliegt. Das liegt daran, daß die Friedel-Summenregel eine Bedingung für die Ladungsabschirmung im Unendlichen darstellt, während über Bereiche in der Nähe der Störstelle nichts ausgesagt wird.