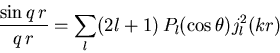

Next: 1.3 Integraldarstellung des Streuproblems
Up: 1 Theoretische Grundlagen der Streuung
Previous: 1.1 Streuwirkungsquerschnitt
Diese schon 1881 von Lord Rayleigh eingeführte Methode benutzt die Eigenschaft, daß sowohl die Streuamplitude 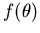 als auch eine ebene Welle
als auch eine ebene Welle 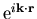 eine Funktion des Streuwinkels
eine Funktion des Streuwinkels 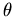 sind, sodaß man sie in Legendre-Polynome folgendermaßen entwickeln kann [AS72]:
sind, sodaß man sie in Legendre-Polynome folgendermaßen entwickeln kann [AS72]:
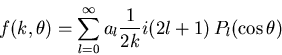 |
(1.5) |
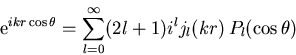 |
(1.6) |
wobei die Koeffizienten al im allgemeinen komplex sind.
Für große r kann man die sphärischen Bessel-Funktionen erster Art jl(kr) schreiben als [AS72]
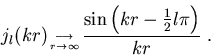 |
(1.7) |
Einsetzen von (1.5), (1.6) und (1.7) in (1.2) ergibt für 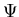 [WO75]
[WO75]
![\begin{displaymath}{\Psi (r,\theta) }_{\longrightarrow \atop r \rightarrow\infty...
...t)}^{l} {\mathrm e}^{-i k r} \right] \, P_{l}(\cos \theta)\; .
\end{displaymath}](img102.gif) |
(1.8) |
Da V(r) sphärisch symmetrisch ist, kann 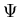 in (1.1) durch einen
Produktansatz weiter vereinfacht werden zu
in (1.1) durch einen
Produktansatz weiter vereinfacht werden zu
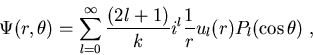 |
(1.9) |
Nach Separation der Winkelabhängigkeit erhalten wir als Radialgleichung für ul(r)
![\begin{displaymath}\frac{d^{2}u_l }{dr^2}+\left[ k^2 -U(r) -\frac{l(l+1)}{r^2} \right] \,u_{l} (r)=0
\end{displaymath}](img105.gif) |
(1.10) |
(1.10) stellt die Bessel-Gleichung dar, deren Lösung
eine Linearkombination der Bessel-Funktionen erster und zweiter Art
darstellen. Um unserem Streuproblem zu genügen, muß ul(r) im Ursprung verschwinden und für große r folgendes Verhalten zeigen:
![\begin{displaymath}
u_{l}(r)_{\longrightarrow \atop r \rightarrow\infty } kr\lef...
...right]=C_{l}\, \sin\left( kr-\frac{l\pi}{2}+\delta_{l} \right)
\end{displaymath}](img106.gif) |
(1.11) |
mit
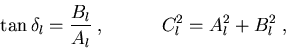 |
(1.12) |
sodaß wir für die Koeffizienten durch Koeffizientenvergleich
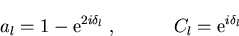 |
(1.13) |
erhalten. nl bezeichnet die sphärischen Bessel-Funktion zweiter Art [AS72].
Damit lautet die Streuamplitude
![\begin{displaymath}
f(k,\theta)= \frac{1}{2 i k}\sum_{l=0}^{\infty} (2l+1) \left[ {\mathrm e}^{2 i \delta_l}-1 \right]\,P_{l}(\cos \theta)
\end{displaymath}](img109.gif) |
(1.14) |
und der differentielle Streuquerschnitt
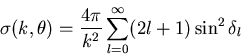 |
(1.15) |
mit
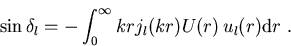 |
(1.16) |
Alle bis jetzt hergeleiteten Relationen sind exakt. Die Phasenverschiebung 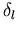 beschreibt die Phasendifferenz zwischen der asymptotischen Lösung
beschreibt die Phasendifferenz zwischen der asymptotischen Lösung
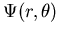 der am Potential V(r) gestreuten Welle und der einer ungestörten Kugelwelle.
der am Potential V(r) gestreuten Welle und der einer ungestörten Kugelwelle.
Man erkennt sofort, daß für ein anziehendes Potential die gestörte
Welle der ungestörten nachläuft, während hingegen für ein abstoßendes Potential die gestörte Welle der ungestörten vorläuft. Im ersten Fall gilt 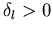 , ansonsten ist
, ansonsten ist 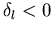 .
Klassisch gilt
.
Klassisch gilt 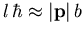 , wobei b der Stoßparameter ist. Die Summation über alle l in (1.14) oder (1.15) ist also äquivalent einer Integration über alle möglichen
Stoßparameter in der klassischen Theorie.
, wobei b der Stoßparameter ist. Die Summation über alle l in (1.14) oder (1.15) ist also äquivalent einer Integration über alle möglichen
Stoßparameter in der klassischen Theorie.
Setzen wir für die gestreute Welle die ungestörte Kugelwelle ein, so erhalten wir die erste Born-Näherung für die Streuphasen
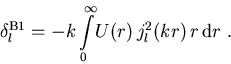 |
(1.17) |
(1.17) gilt, falls die Phasen für alle l klein gegenüber
eins sind. Wir können dann in (1.14) die Exponentialfunktion bis erster Ordnung entwickeln, sodaß
wir für (1.14) erhalten
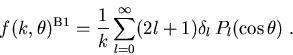 |
(1.18) |
Die Reihe kann unter Zuhilfenahme von
[AS72]
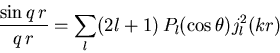 |
(1.19) |
aufsummiert werden und liefert die bekannte Born-Streuamplitude erster Ordnung
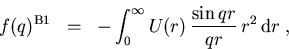 |
(1.20) |
wobei
wir den Impulsübertrag 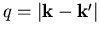 des gestreuten Elektrons eingeführt haben, da in der Born-Näherung die Streuamplitude nur vom Impulsübertrag abhängt.
Interessanterweise erfüllen die Streuphasen
des gestreuten Elektrons eingeführt haben, da in der Born-Näherung die Streuamplitude nur vom Impulsübertrag abhängt.
Interessanterweise erfüllen die Streuphasen 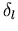 (1.17) die Friedel-Summenregel (Anhang E), wenn man als Störpotential ein exponentiell geschirmtes Coulomb-Potential annimmt. Diese Regel über die Summe aller zusätzlichen Energiezustände, die eine Störstelle in einem
Festkörper erzeugt, stellt eine
Art Erhaltungssatz für die Ladung in einem Festkörper dar.
(1.17) die Friedel-Summenregel (Anhang E), wenn man als Störpotential ein exponentiell geschirmtes Coulomb-Potential annimmt. Diese Regel über die Summe aller zusätzlichen Energiezustände, die eine Störstelle in einem
Festkörper erzeugt, stellt eine
Art Erhaltungssatz für die Ladung in einem Festkörper dar.


Next: 1.3 Integraldarstellung des Streuproblems
Up: 1 Theoretische Grundlagen der Streuung
Previous: 1.1 Streuwirkungsquerschnitt
Kaiblinger-Grujin Goran
1997-12-06
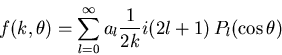
![\begin{displaymath}{\Psi (r,\theta) }_{\longrightarrow \atop r \rightarrow\infty...
...t)}^{l} {\mathrm e}^{-i k r} \right] \, P_{l}(\cos \theta)\; .
\end{displaymath}](img102.gif)
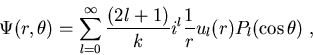
![\begin{displaymath}\frac{d^{2}u_l }{dr^2}+\left[ k^2 -U(r) -\frac{l(l+1)}{r^2} \right] \,u_{l} (r)=0
\end{displaymath}](img105.gif)
![]() , ansonsten ist
, ansonsten ist ![]() .
Klassisch gilt
.
Klassisch gilt ![]() , wobei b der Stoßparameter ist. Die Summation über alle l in (1.14) oder (1.15) ist also äquivalent einer Integration über alle möglichen
Stoßparameter in der klassischen Theorie.
, wobei b der Stoßparameter ist. Die Summation über alle l in (1.14) oder (1.15) ist also äquivalent einer Integration über alle möglichen
Stoßparameter in der klassischen Theorie.