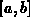 defined with the aid of a sequence of non decreasing
points, the so-called knot sequence
defined with the aid of a sequence of non decreasing
points, the so-called knot sequence 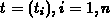 with
with 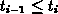 .
B-splines are defined using divided differences. Given an integer
.
B-splines are defined using divided differences. Given an integer 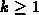 and a non-decreasing knot sequence
and a non-decreasing knot sequence 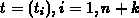 , the
, the 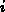 th B-spline
of order k for the knot sequence
th B-spline
of order k for the knot sequence 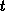 is denoted by
is denoted by 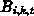 and is given
by [14]:
and is given
by [14]:






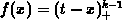 is the piecewise truncated power function
of order k
is the piecewise truncated power function
of order k 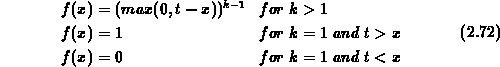
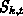 . Any polynomial spline function
. Any polynomial spline function 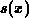 of order k in
of order k in
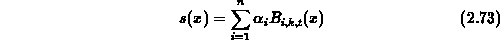
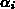 can be selected so as to enforce specific
conditions on the spline function. For instance by enforcing that the spline
function agrees with a given data set values
(
can be selected so as to enforce specific
conditions on the spline function. For instance by enforcing that the spline
function agrees with a given data set values
(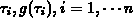 ) we get the spline interpolation
conditions:
) we get the spline interpolation
conditions:
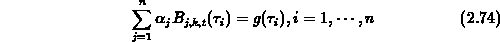
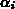 's.
The system is invertible provided that:
's.
The system is invertible provided that:
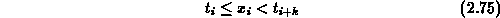
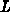 and the nonlinear least squares objective as
follows:
and the nonlinear least squares objective as
follows:
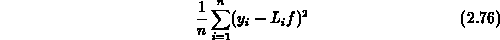
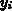 's are the observed functional values and
's are the observed functional values and
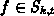 a properly selected subspace with basis function
a properly selected subspace with basis function
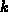 and general qualitative properties such as the smoothness
of the function
and general qualitative properties such as the smoothness
of the function 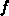 can be determined based on expectations
about the solution in a straightforward fashion. However,
specifying the appropriate knot sequence (
can be determined based on expectations
about the solution in a straightforward fashion. However,
specifying the appropriate knot sequence (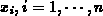 for the spline function
for the spline function
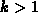 by:
by:
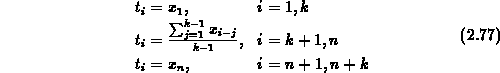
 first
derivatives in
first
derivatives in 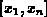 .
.