


Next: 4.4 Rekombination im Drift-Diffusionsmodell
Up: 4 Gittertemperaturabhängige Rekombination/Generation
Previous: 4.2 Die Gleichung der
Die statische Rekombinationsgleichung erhält man aus der dynamischen, indem man in (4.5) dnt/dt=0 setzt.
Da sich die lokale Besetzungsfunktion fo mit der Zeit nicht ändert, müssen die Nettorekombinationsraten der
Elektronen und Löcher gleich sein
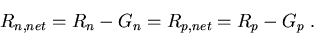 |
(4.20) |
Die Größen Np,eff,Nn,eff kann man über das intrinsische Niveau ausdrücken
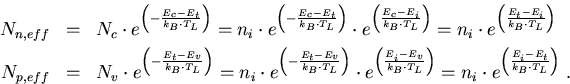 |
(4.21) |
Schreibt man die Nettoraten (4.20) explizit an, so erhält man mit (4.14),(4.17)
![\begin{eqnarray}
R_{net}&=&\sigma_n\cdot v_{th,n}\cdot N_t\left[n\cdot(1-f_o)-f_...
..._o)\cdot e^{\left(\frac{E_i-E_t}{k_B\cdot T_L}\right)}\right]\; .
\end{eqnarray}](img285.gif) |
(4.22) |
Löst man (4.22) nach fo auf, erhält man
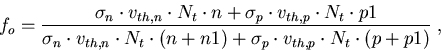 |
(4.23) |
wobei die Abkürzungen
 |
(4.24) |
verwendet wurden.
Setzt man (4.23) in die rechte Seite von (4.22) ein, so erhält man
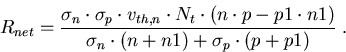 |
(4.25) |
Division durch 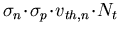 ergibt die klassische stationäre Form der
Nettorekombinationsrate
ergibt die klassische stationäre Form der
Nettorekombinationsrate
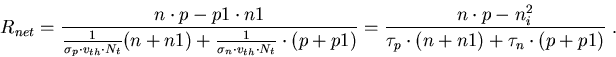 |
(4.26) |
Die Größen 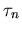 und
und 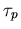 bezeichnet man üblicherweise als Lebensdauer der Elektronen bzw. Löcher. Bei
konstanter thermischer Geschwindigkeit ist die Lebensdauer eines Ladungsträgers umso größer, je geringer die
Fehlstellendichte ist. Im Gegensatz dazu geben die Einfangzeiten in (4.8) jene Zeit an, in der im Mittel
eine Fehlstelle einen Ladungsträger einfängt. Die Einfangzeit ist umso größer, je kleiner die Konzentration der
freien Ladungsträger ist. Gleichung (4.26) beschreibt den stationären Generations/Rekombinationsprozeß,
der auch oft als stationärer SHOCKLEY-READ-HALL-Prozeß (SRH) bezeichnet wird.
Die Abhängigkeit der Lebensdauern
bezeichnet man üblicherweise als Lebensdauer der Elektronen bzw. Löcher. Bei
konstanter thermischer Geschwindigkeit ist die Lebensdauer eines Ladungsträgers umso größer, je geringer die
Fehlstellendichte ist. Im Gegensatz dazu geben die Einfangzeiten in (4.8) jene Zeit an, in der im Mittel
eine Fehlstelle einen Ladungsträger einfängt. Die Einfangzeit ist umso größer, je kleiner die Konzentration der
freien Ladungsträger ist. Gleichung (4.26) beschreibt den stationären Generations/Rekombinationsprozeß,
der auch oft als stationärer SHOCKLEY-READ-HALL-Prozeß (SRH) bezeichnet wird.
Die Abhängigkeit der Lebensdauern 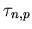 von der Gittertemperatur TL ist nach [55] implementiert
von der Gittertemperatur TL ist nach [55] implementiert
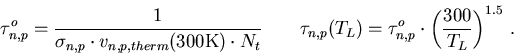 |
(4.27) |
Aus Gleichung (4.26) erkennt man, daß die Generation von Ladungsträgern bei einer Annahme von 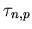 durch ni2 begrenzt ist. Liegt Rekombination vor, so hängt die maximale Rekombinationsrate von dem Produkt aus
durch ni2 begrenzt ist. Liegt Rekombination vor, so hängt die maximale Rekombinationsrate von dem Produkt aus
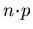 ab, welches im Gegensatz zu ni2 beliebig groß werden kann. Der Ableitung von Gleichung
(4.26) liegt jedoch die Annahme zugrunde, daß die Anzahl der am Rekombinationsprozeß teilnehmenden
Ladungsträger wesentlich kleiner ist, als die Fehlstellenanzahl Nt. Dadurch ist es möglich, in der Herleitung
von (4.26) die Umordnungszeiten der Fehlstelleatome zu vernachlässigen. Übersteigen die Konzentrationen der
freien Ladungsträger die Fehlstellenkonzentration, so wird der Rekombinationsprozeß durch die Umordnungszeiten der
Fehlstellen mitbeeinflußt. Die tatsächliche auftretende Rekombinationsrate sättigt deshalb für hohe
Ladungsträgerkonzentrationen im Gegensatz zu (4.26). Eine Behandlung dieser Thematik kann in
[16,59] nachgelesen werden.
ab, welches im Gegensatz zu ni2 beliebig groß werden kann. Der Ableitung von Gleichung
(4.26) liegt jedoch die Annahme zugrunde, daß die Anzahl der am Rekombinationsprozeß teilnehmenden
Ladungsträger wesentlich kleiner ist, als die Fehlstellenanzahl Nt. Dadurch ist es möglich, in der Herleitung
von (4.26) die Umordnungszeiten der Fehlstelleatome zu vernachlässigen. Übersteigen die Konzentrationen der
freien Ladungsträger die Fehlstellenkonzentration, so wird der Rekombinationsprozeß durch die Umordnungszeiten der
Fehlstellen mitbeeinflußt. Die tatsächliche auftretende Rekombinationsrate sättigt deshalb für hohe
Ladungsträgerkonzentrationen im Gegensatz zu (4.26). Eine Behandlung dieser Thematik kann in
[16,59] nachgelesen werden.



Next: 4.4 Rekombination im Drift-Diffusionsmodell
Up: 4 Gittertemperaturabhängige Rekombination/Generation
Previous: 4.2 Die Gleichung der
Martin Knaipp
1998-10-09