


Next: 4.5 Beispiel einer Leckstromsimulation
Up: 4 Gittertemperaturabhängige Rekombination/Generation
Previous: 4.3 Die statische Rekombinationsgleichung
Rekombination im DD- und HD-Modell
4.4 Rekombination im Drift-Diffusionsmodell
und im hydrodynamischen Modell
Gleichung (4.26) berechnet die lokale Nettorekombinationsrate, die sich durch das Gleichgewicht zwischen
Generation und Rekombination einstellt. Dabei beschreibt das Produkt aus 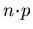 im ersten Summanden des
Zählers von (4.26) den Anteil der Ladungsträgerrekombination. Ist dieses Produkt größer als ni2, so ist
Rnet positiv, d.h. es rekombinieren Trägerpaare. Bilden sich Raumladungszonen im Bauteil aus, so verschwinden
die freien Ladungsträger und der Summand ni2 ist maßgebend für die Ladungsträgergeneration. In der Ableitung
der Lebensdauern
im ersten Summanden des
Zählers von (4.26) den Anteil der Ladungsträgerrekombination. Ist dieses Produkt größer als ni2, so ist
Rnet positiv, d.h. es rekombinieren Trägerpaare. Bilden sich Raumladungszonen im Bauteil aus, so verschwinden
die freien Ladungsträger und der Summand ni2 ist maßgebend für die Ladungsträgergeneration. In der Ableitung
der Lebensdauern 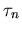 und
und 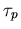 kommt als unabhängige Variable die thermische Geschwindigkeit vor. Diese
errechnet sich im Drift-Diffusionsmodell aus der Gittertemperatur, während sie im hydrodynamischen Modell aus der Trägertemperatur
berechnet wird, welche in Raumladungszonen wesentlich höhere Werte annehmen kann. Das klassische
Rekombinationsmodell (4.26) wurde ursprünglich im Drift-Diffusionsmodell angewendet, wo ausschließlich die
Gittertemperatur bekannt ist.
Die Ladungsträgertemperatur im hydrodynamischen Modell hängt in erster Näherung von der lokalen Feldstärke im Bauteil ab. In
feldfreien Bereichen, wo Rekombination auftreten kann, liegt sie nahe an der Gittertemperatur. In Raumladungszonen,
wo hauptsächlich Ladungsträgergeneration auftritt, kann sie im Bereich der Gittertemperatur und einigen tausend
Kelvin liegen. Gerade hier stellt sich die Frage, inwieweit es sinnvoll ist, die Emission eines gebundenen
Ladungsträgers durch die lokale thermische Geschwindigkeit von möglichen freien Ladungsträgern zu beschreiben. Da
der Energiefluß aufgrund der geringen Stromdichte klein ist, tritt in Raumladungszonen so gut wie keine
Gittererwärmung auf. Es liegt also nahe, auch im hydrodynamischen Modell die Generationsprozesse durch die lokale
Gittertemperatur zu beschreiben. Dadurch ist gewährleistet, daß die Emissionszeiten (4.9) in
Raumladungsgebieten mit konstanter Fehlstellendichte und Fehlstellenenergieniveau konstant sind. Allerdings ist eine
physikalische Interpretation von (4.8) in Raumladungsgebieten nicht mehr möglich.
Gleichung (4.26) ist eine Bilanzgleichung, die das Gleichgewicht zweier mikroskopischer Vorgänge ausdrückt.
Rekombinations- und Generationsvorgänge sind im allgemeinen so komplexe Vorgänge, daß sie nur durch
quantenmechanische Effekte erklärbar sind. So ist bei einer hohen Dotierung das Wirken der Fehlstellen nicht mehr
unabhängig von der Dotierung. Dabei können mehrere lokale Fehlstellen die Bandstruktur so verändern, daß die
Wirkung jeder einzelnen Fehlstelle verstärkt wird. Diese Effekte kann man berücksichtigen, indem die Lebensdauern
kommt als unabhängige Variable die thermische Geschwindigkeit vor. Diese
errechnet sich im Drift-Diffusionsmodell aus der Gittertemperatur, während sie im hydrodynamischen Modell aus der Trägertemperatur
berechnet wird, welche in Raumladungszonen wesentlich höhere Werte annehmen kann. Das klassische
Rekombinationsmodell (4.26) wurde ursprünglich im Drift-Diffusionsmodell angewendet, wo ausschließlich die
Gittertemperatur bekannt ist.
Die Ladungsträgertemperatur im hydrodynamischen Modell hängt in erster Näherung von der lokalen Feldstärke im Bauteil ab. In
feldfreien Bereichen, wo Rekombination auftreten kann, liegt sie nahe an der Gittertemperatur. In Raumladungszonen,
wo hauptsächlich Ladungsträgergeneration auftritt, kann sie im Bereich der Gittertemperatur und einigen tausend
Kelvin liegen. Gerade hier stellt sich die Frage, inwieweit es sinnvoll ist, die Emission eines gebundenen
Ladungsträgers durch die lokale thermische Geschwindigkeit von möglichen freien Ladungsträgern zu beschreiben. Da
der Energiefluß aufgrund der geringen Stromdichte klein ist, tritt in Raumladungszonen so gut wie keine
Gittererwärmung auf. Es liegt also nahe, auch im hydrodynamischen Modell die Generationsprozesse durch die lokale
Gittertemperatur zu beschreiben. Dadurch ist gewährleistet, daß die Emissionszeiten (4.9) in
Raumladungsgebieten mit konstanter Fehlstellendichte und Fehlstellenenergieniveau konstant sind. Allerdings ist eine
physikalische Interpretation von (4.8) in Raumladungsgebieten nicht mehr möglich.
Gleichung (4.26) ist eine Bilanzgleichung, die das Gleichgewicht zweier mikroskopischer Vorgänge ausdrückt.
Rekombinations- und Generationsvorgänge sind im allgemeinen so komplexe Vorgänge, daß sie nur durch
quantenmechanische Effekte erklärbar sind. So ist bei einer hohen Dotierung das Wirken der Fehlstellen nicht mehr
unabhängig von der Dotierung. Dabei können mehrere lokale Fehlstellen die Bandstruktur so verändern, daß die
Wirkung jeder einzelnen Fehlstelle verstärkt wird. Diese Effekte kann man berücksichtigen, indem die Lebensdauern
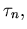 und
und 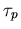 durch geeignete Modelle reduziert werden [14,21,22,32]
durch geeignete Modelle reduziert werden [14,21,22,32]
 |
(4.28) |
Die dabei verwendeten Referenzkonzentrationen Nref,n,Nref,p liegen im Bereich von 1016 bis
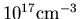 , bei Referenzlebensdauern
, bei Referenzlebensdauern 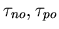 von 10-6 bis 10-4s.
von 10-6 bis 10-4s.



Next: 4.5 Beispiel einer Leckstromsimulation
Up: 4 Gittertemperaturabhängige Rekombination/Generation
Previous: 4.3 Die statische Rekombinationsgleichung
Martin Knaipp
1998-10-09
