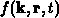 basiert auf der Einteilchen-Dichtematrix, die folgendermaßen
definiert ist,
basiert auf der Einteilchen-Dichtematrix, die folgendermaßen
definiert ist,




Die Definition der quantenmechanischen Verteilungsfunktion 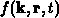 basiert auf der Einteilchen-Dichtematrix, die folgendermaßen
definiert ist,
basiert auf der Einteilchen-Dichtematrix, die folgendermaßen
definiert ist,
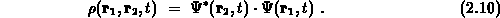
Da die zeitliche Entwicklung von 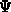 durch eine
Schrödingergleichung
beschrieben wird, läßt sich unmittelbar auch die zeitliche
Entwicklung von
durch eine
Schrödingergleichung
beschrieben wird, läßt sich unmittelbar auch die zeitliche
Entwicklung von 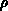 angeben,
angeben,
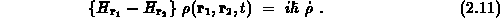
Das ist die Liouville-Von-Neumann-Gleichung.
Darin bedeutet 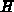 den Hamiltonoperator, wie er auf der linken Seite von
Gleichung 2.7 vorkommt. Der Operator
den Hamiltonoperator, wie er auf der linken Seite von
Gleichung 2.7 vorkommt. Der Operator 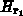 soll nur auf die
Koordinate
soll nur auf die
Koordinate 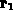 in
in 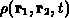 wirken,
wirken, 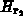 nur auf
nur auf 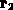 .
.
Im folgenden setzen wir den Hamiltonoperator aus Gleichung 2.7 ein, wobei das Streupotential vernachlässigt werden soll. Dieses soll am Ende der Ableitung durch Einführung eines Quellterms wieder berücksichtigt werden,
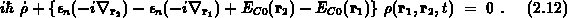
Zur weiteren Umformung ist eine Koordinatentransformation sinnvoll, durch die man auf Schwerpunkts- und Relativkoordinaten übergeht,
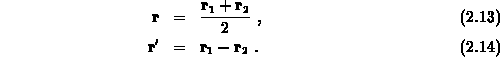
Ändert sich das äußere Potential im Vergleich zur Wellenlänge des Elektrons nur wenig, so erscheint die folgende Linearisierung gerechtfertigt,
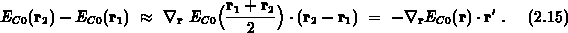
Der negative Gradient des Feldes der potentiellen Energie ergibt ein Kraftfeld, das auf die Elektronen wirkt. Das Ergebnis der Linearisierung ist
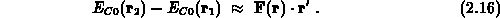
Durch die Koordinatentransformation transformieren sich auch die Gradienten,
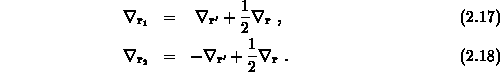
Die Differenz der Operatoren für die kinetische Energie läßt sich unter der
Voraussetzung, daß das Elektron auch im 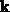 -Raum gut lokalisiert ist,
ebenfalls linearisieren,
-Raum gut lokalisiert ist,
ebenfalls linearisieren,
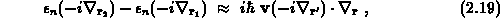
wobei für den Gradient 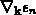 die
Gruppengeschwindigkeit
die
Gruppengeschwindigkeit 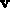 eingesetzt wurde.
Die Dichtematrix in den neuen Koordinaten nennen wir
eingesetzt wurde.
Die Dichtematrix in den neuen Koordinaten nennen wir 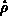 ,
,
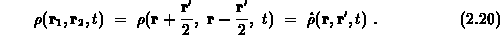
Damit erhält die Liouville-Von-Neumann-Gleichung die Form
Die quantenmechanische Verteilungsfunktion erhält man aus der
Einteilchen-Dichtematrix
durch Fouriertransformation bezüglich der Relativkoordinate 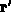 ,
,
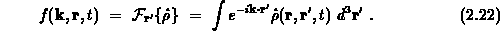
Physikalisch bedeutet das den Übergang von der Ortsdarstellung in die Impulsdarstellung. Anwenden der Fouriertransformation auf die Terme von Gleichung 2.21 liefert
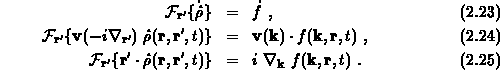
Setzt man diese Beziehungen ein und dividiert durch 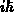 ,
ergibt sich die homogene Boltzmanngleichung
,
ergibt sich die homogene Boltzmanngleichung
Der erste Term ist nur bei zeitabhängigen Anwendungen von Bedeutung und verschwindet im stationären Fall. Der zweite Term wird als Diffusionsterm interpretiert, da er die räumliche Änderung der Verteilungsfunktion berücksichtigt. Der dritte Term enthält das Kraftfeld, unter dessen Einfluß sich die Teilchen bewegen, und wird daher als Driftterm bezeichnet.



