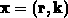 gegeben, die Geschwindigkeit durch
gegeben, die Geschwindigkeit durch
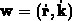 .
Die Kontinuitätsgleichung für diese Dichte kann nun geschrieben werden als
.
Die Kontinuitätsgleichung für diese Dichte kann nun geschrieben werden als




Die Boltzmanngleichung kann auch als Kontinuitätsgleichung im sechs dimensionalen
Einteilchen-Phasenraum aufgefaßt werden. Die Dichte im Phasenraum
ist die
Verteilungsfunktion f(k,r ,t), ein Punkt ist durch den sechskomponentigen Vektor
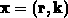 gegeben, die Geschwindigkeit durch
gegeben, die Geschwindigkeit durch
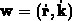 .
Die Kontinuitätsgleichung für diese Dichte kann nun geschrieben werden als
.
Die Kontinuitätsgleichung für diese Dichte kann nun geschrieben werden als
Der Quellterm auf der rechten Seite muß dann berücksichtigt werden, wenn sich der Zustand eines Teilchens nicht nur kontinuierlich, also entlang einer Trajektorie im Phasenraum, ändern kann, sondern wenn auch abrupte Zustandsänderungen, etwa durch Streuprozesse, möglich sind. Eine klassische Interpretation der Streuzentren als innere Kräfte, die genau durch diesen Quellterm beschrieben werden, findet sich in [93].
Die Divergenz 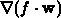 kann nach der Produktregel zerlegt
werden in
kann nach der Produktregel zerlegt
werden in
Die Geschwindigkeit 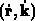 im Phasenraum ist gegeben durch
die Hamiltonschen Bewegungsgleichungen
im Phasenraum ist gegeben durch
die Hamiltonschen Bewegungsgleichungen
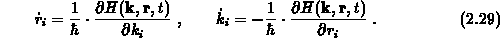
Daraus folgt, daß der Ausdruck 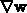 in der Gleichung
2.28 null ist,
in der Gleichung
2.28 null ist,
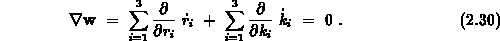
Der verbleibende Term 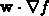 kann nun wieder
durch drei dimensionale Vektoren ausgedrückt werden
kann nun wieder
durch drei dimensionale Vektoren ausgedrückt werden
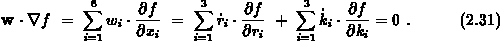
Darin bedeutet 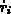 die Geschwindigkeit des Teilchens
die Geschwindigkeit des Teilchens

und für die 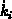 gilt das Newtonsche Gesetz
gilt das Newtonsche Gesetz
Faßt man die Gleichungen 2.27 bis 2.33 zusammen, so erhält man die Boltzmanngleichung in der Form
Man kann sich leicht davon überzeugen, daß die linke Seite dieser
Gleichung die vollständige Zeitableitung von
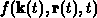 darstellt. Die Boltzmanngleichung kann daher auch
in der kurzen, kompakten Formulierung
darstellt. Die Boltzmanngleichung kann daher auch
in der kurzen, kompakten Formulierung
angeschrieben werden.