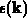Zur Ermittlung der Gruppengeschwindigkeit muß zunächst die
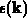-Beziehung nach dem Wellenvektor differenziert werden,
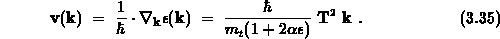
Führt man wieder die Herring-Vogt-Transformation durch
(
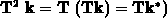, so wird
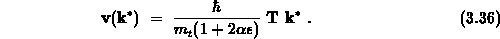
Den Nenner in dieser Gleichung bezeichnet man als Leitfähigkeits-effektive-Masse
Diese Masse ist energie- und somit auch zeitabhängig. Für die
Zeitintegration wird sie jedoch innerhalb eines
Diskretisierungsvolumens als konstant angenommen, um einfachere
Ausdrücke zu erhalten.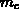 
wird nach jedem Streuprozeß und bei jedem
Übergang in eine benachbarte Zelle an die Energie angepaßt.
Die Bewegungsgleichung 3.28 wird mit dieser Annahme linear in der
Zeit
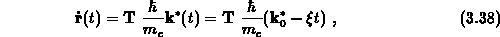
und läßt sich somit einfach integrieren gemäß
Die Bahnen im Ortsraum sind also wie bei klassischen Teilchen Parabeln, wobei die Masse aber vom jeweiligen Energiebereich abhängt.
Da ein freier Flug sich über mehrere Gitterzellen erstrecken und auch
Reflexionen an einem Rand einschließen kann, müssen die genauen
Übertrittszeitpunkte zwischen den Zellen beziehungsweise die genauen
Reflexionszeitpunkte ermittelt werden. Geometrieabfragen, die in den einzelnen
Koordinatenrichtungen unabhängig voneinander durchgeführt werden können,
liefern die Abstände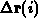 
zu den jeweils nächsten Rändern.
Anschließend ist für jede Richtung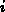 
die Gleichung 3.39 umzukehren.
Dies erfordert die Lösung der quadratischen Gleichung
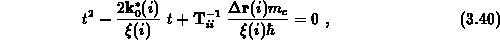
Würde man die
Annahme einer konstanten Leitfähigkeits-effektiven Masse nicht treffen,
so ließe sich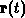 
analytisch auswerten, jedoch wäre die
Umkehrung des so erhaltenen Ausdruckes nicht mehr analytisch möglich.
Die numerische Auswertung würde die ohnehin hohe Rechenzeit eines
Monte-Carlo-Programmes noch wesentlich erhöhen.
