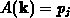In diesem Abschnitt soll die Drift-Diffusionsstromgleichung aus der ersten Momentengleichung hergeleitet und auf die dabei getroffenen Annahmen eingegangen werden.
Den Ausgangspunkt bildet die allgemeine Momentengleichung
Gleichung 4.13 mit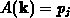 
.
Die beiden Mittelwerte auf der linken Seite nehmen dann folgende Gestalt an,
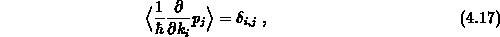
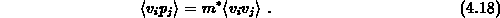
Im letzten Ausdruck wurde die Konstante-effektive-Masse-Näherung verwendet.
Das Streuintegral auf der rechten Seite wird durch die Gleichung 4.16
mit einer Impulsrelaxationszeit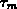 
angenähert.
Wegen der Symmetrie der Verteilungsfunktion verschwindet
die mittlere Geschwindigkeit im Relaxationszeitansatz im thermodynamischen
Gleichgewicht,
Führt man die Definitionen für die Beweglichkeit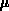 
und die
Stromdichte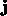 
ein,
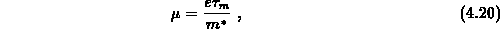
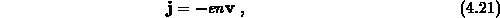
so gelangt man zu einer Stromgleichung der Form
Um diese auch verwenden zu können, muß noch eine Annahme über das
vorkommende Moment 2.Ordnung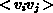 
getroffen werden.
Da es sich um eine tensorielle Größe handelt, versucht man mit Hilfe der
Spur eine skalare Größe als Näherung zu finden,
worin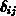 
das Kronecker-Symbol bedeutet.
Andererseits ist in der verwendeten Effektive-Masse-Näherung die Energie eines Teilchens gegeben durch
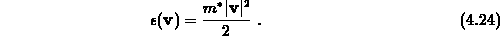
Somit kann die Näherung 4.23 auch durch die mittlere Energie ausgedrückt werden
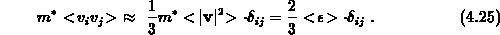
Über die Beziehung
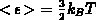kann man aus der mittleren Energie eine Trägertemperatur definieren.
Jedoch ist dies keine Temperatur im thermodynamischen Sinn, da die Verteilungsfunktion
im Nichtgleichgewichtsfall von der Maxwellverteilung abweicht und daher
eine Temperatur zu ihrer vollständigen Beschreibung nicht mehr aussreicht.
Setzt man die beschriebenen Näherungen ein, so läßt sich die Stromgleichung 4.22 schreiben als
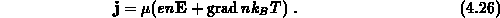
Durch die Einführung der Temperaturspannung
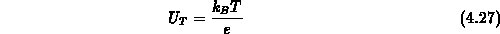
gelangt man zu der folgenden Notation, von der im weiteren ausgegangen werden soll,
Diese Gleichung wird oft als erweiterte Drift-Diffusionsgleichung bezeichnet, da sie eine variable Temperaturspannung zuläßt.
Eine etwas andere Ableitung, die zu derselben Stromgleichung führt, findet sich bei Hänsch [33],[34],[38]. Dabei wird die Verteilungsfunktion nach den ersten vier Momenten entwickelt und dann die Momentengleichungen gebildet.
Beim klassischen Drift-Diffusionsmodell wird zusätzlich angenommen, daß sich die Elektronen im thermodynamischen Gleichgewicht mit dem Kristallgitter befinden. Es gilt also
Unter dieser Voraussetzung gilt für den Diffusionskoeffizienten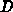 
auch die Einsteinrelation
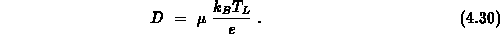
Auf diese Weise wird aus der Stromgleichung 4.28 die klassische Drift-Diffusionsgleichung, die sich für Elektronen schreiben läßt als [93]
