5.1 Das Prinzip der Selbststreuung




Next: 5.2 Ein verbesserter Selbststreualgorithmus
Up: 5 Numerische Aspekte
Previous: 5 Numerische Aspekte
Im Abschnitt 4.3.1 wurden die Grundlagen zur Berechnung der
freien Flugdauer dargestellt. Als Bestimmungsgleichung für die freie
Flugdauer wurde die Integralgleichung 4.35 erhalten.
Führt man eine Zeitdiskretisierung ein, die der Bedingung 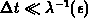 genügt, so kann diese Integralgleichung
direkt
verwendet werden, indem man die Integration numerisch ausführt.
Dies ist vor allen in jenen Fällen sinnvoll, in denen
genügt, so kann diese Integralgleichung
direkt
verwendet werden, indem man die Integration numerisch ausführt.
Dies ist vor allen in jenen Fällen sinnvoll, in denen 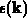 und
und
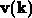 numerisch gegeben sind und die Bewegungsgleichungen zeitdiskret
gelöst werden müssen.
numerisch gegeben sind und die Bewegungsgleichungen zeitdiskret
gelöst werden müssen.
Ist 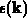 jedoch wie in der vorliegenden Arbeit analytisch gegeben,
so ist eine analytische Lösung der Bewegungsgleichungen möglich
(vergleiche Abshnitt 3.2).
Somit kann der Zustand am Ende des freien Fluges zum Zeitpunkt
jedoch wie in der vorliegenden Arbeit analytisch gegeben,
so ist eine analytische Lösung der Bewegungsgleichungen möglich
(vergleiche Abshnitt 3.2).
Somit kann der Zustand am Ende des freien Fluges zum Zeitpunkt 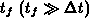 direkt berechnet werden, ohne Zustände an den
dazwischenliegenden Zeitpunkten
direkt berechnet werden, ohne Zustände an den
dazwischenliegenden Zeitpunkten 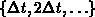 berechnen
zu müssen.
berechnen
zu müssen.
Für eine analytische 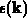 -Beziehung ist also eine analytische
Lösung der Integralgleichung für die freie Flugdauer wünschenswert.
Genau das kann durch Einführung eines zusätzlichen
Streumechanismus der Form
-Beziehung ist also eine analytische
Lösung der Integralgleichung für die freie Flugdauer wünschenswert.
Genau das kann durch Einführung eines zusätzlichen
Streumechanismus der Form
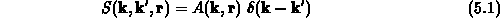
erreicht werden. Die 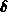 -Funktion bewirkt, daß bei dieser Streuung
keine Änderung des Zustandes
-Funktion bewirkt, daß bei dieser Streuung
keine Änderung des Zustandes 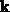 erfolgt, weshalb man auch von
Selbststreuung spricht [82]. Die Freiheit in der Wahl der Amplitude
erfolgt, weshalb man auch von
Selbststreuung spricht [82]. Die Freiheit in der Wahl der Amplitude 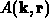 verwendet man nun dazu,
die totale Streurate zu einer Konstanten
verwendet man nun dazu,
die totale Streurate zu einer Konstanten 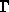 zu machen.
Damit wird der Integrand in Gleichung 4.35 von (k,r) unabhängig, und
zu machen.
Damit wird der Integrand in Gleichung 4.35 von (k,r) unabhängig, und
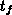 kann einfach bestimmt werden durch
kann einfach bestimmt werden durch
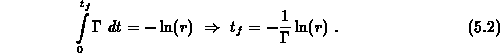
Die Einführung der Selbststreuung führt in diesem Fall zu einem
einfachen funktionalen Zusammenhang zwischen der freien Flugdauer 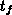 und
der Zufallszahl
und
der Zufallszahl  .
.
Ein Nachteil dieser Methode resultiert daraus, daß die physikalische Streurate
im Orts- und Energiebereich stark variiert. 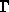 muß aber eine obere
Schranke von
muß aber eine obere
Schranke von 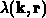 für alle in der Simulation möglichen
für alle in der Simulation möglichen
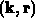 sein. Befindet sich etwa das Elektron in einem Energiebereich,
wo die Streurate klein ist, so werden nach Gleichung 5.2 trotzdem sehr
kleine Flugzeiten erzeugt, da
sein. Befindet sich etwa das Elektron in einem Energiebereich,
wo die Streurate klein ist, so werden nach Gleichung 5.2 trotzdem sehr
kleine Flugzeiten erzeugt, da 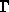 nach der maximalen Streurate
ausgerichtet ist. Das Verfahren erzeugt deshalb in bestimmten Energiebereichen
eine große Anzahl von Selbststreuprozessen, bevor ein physikalischer
Streuprozeß eintritt.
nach der maximalen Streurate
ausgerichtet ist. Das Verfahren erzeugt deshalb in bestimmten Energiebereichen
eine große Anzahl von Selbststreuprozessen, bevor ein physikalischer
Streuprozeß eintritt.
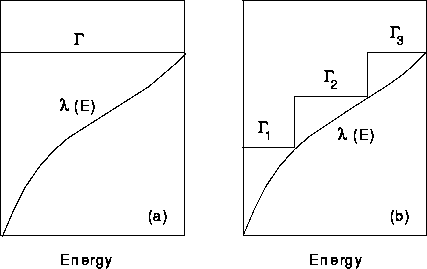
Abbildung: Totale Streuraten einschließlich Selbststreuung:
(a) totale Streurate 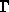 unabhängig von der Energie,
(b) treppenförmige totale Streurate.
unabhängig von der Energie,
(b) treppenförmige totale Streurate.
In Abbildung 5.1 ist das Verhältnis von realer Streurate
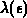 zu
Selbststreurate
zu
Selbststreurate 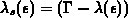 schematisch dargestellt.
Der hohe
Selbststreuanteil bei niedrigen Energien kann durch einen Übergang auf eine
stückweise konstante Begrenzungsfunktion reduziert werden
(Abbildung 5.1 (b)).
Da die Trajektorie durch Bereiche mit verschiedenen
schematisch dargestellt.
Der hohe
Selbststreuanteil bei niedrigen Energien kann durch einen Übergang auf eine
stückweise konstante Begrenzungsfunktion reduziert werden
(Abbildung 5.1 (b)).
Da die Trajektorie durch Bereiche mit verschiedenen 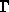 -Werten laufen
kann, müssen die genauen Zeitpunkte für die Übergänge berechnet werden,
womit sich der Rechenaufwand erhöht.
-Werten laufen
kann, müssen die genauen Zeitpunkte für die Übergänge berechnet werden,
womit sich der Rechenaufwand erhöht.
Moglestue [70] schlägt zur Reduktion der Selbststreuprozesse ein
adaptives Verfahren vor, in dem für den augenblicklichen Energiezustand
und die augenblickliche Zufallszahl ein möglichst kleines 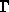 gewählt
wird. Die Wahl der Flugdauer erfolgt dabei konsistent mit der anschließenden
Auswahl des Streuprozesses. Die sehr komfortable Mittelwertbildung mit Hilfe
der sogenannte ,,before scattering``-Methode (Abschnitt 4.3.3)
ist jedoch nicht mehr anwendbar, da keine eindeutige
gewählt
wird. Die Wahl der Flugdauer erfolgt dabei konsistent mit der anschließenden
Auswahl des Streuprozesses. Die sehr komfortable Mittelwertbildung mit Hilfe
der sogenannte ,,before scattering``-Methode (Abschnitt 4.3.3)
ist jedoch nicht mehr anwendbar, da keine eindeutige
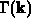 -Abhängigkeit existiert.
-Abhängigkeit existiert.
Kato [53] verwendet ein anderes Optimierungsverfahren zur
Ermittlung eines angepaßten 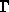 . Für den Fall, daß
. Für den Fall, daß 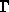 zu
klein gewählt wurde, wird durch eine
zu
klein gewählt wurde, wird durch eine 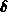 -förmige Selbststreurate ein
Selbststreuprozeß erzwungen. Für die Mittelwertbildung gilt ebenfalls die
im obigen Verfahren beschriebene Einschränkung.
-förmige Selbststreurate ein
Selbststreuprozeß erzwungen. Für die Mittelwertbildung gilt ebenfalls die
im obigen Verfahren beschriebene Einschränkung.
Die Implementierung
einer gut angepaßte Treppenfunktion
nach Abbildung 5.1 (b)
in einen Bauelemente-Simulator
wird in [91] beschrieben.
Wegen
der örtlich veränderlichen Störstellenstreuung wurden
auch die einzelnen
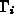 ortsabhängig gewählt. Die Mittelwerte können
mit der ,,before scattering``-Methode
gebildet werden. Durch Verwendung kleiner Energieintervalle kann die
Selbststreurate wirkungsvoll reduziert werden, jedoch erhöht sich der
Rechenaufwand. Die Anzahl der Parameter zur Beschreibung der orts- und
energieabhängigen Treppenfunktion dürfte relativ hoch sein.
Dieses Verfahren hat ebenso wie das mit durchgehend konstantem
ortsabhängig gewählt. Die Mittelwerte können
mit der ,,before scattering``-Methode
gebildet werden. Durch Verwendung kleiner Energieintervalle kann die
Selbststreurate wirkungsvoll reduziert werden, jedoch erhöht sich der
Rechenaufwand. Die Anzahl der Parameter zur Beschreibung der orts- und
energieabhängigen Treppenfunktion dürfte relativ hoch sein.
Dieses Verfahren hat ebenso wie das mit durchgehend konstantem 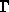 den
Nachteil, daß im Fall monoton steigender Streuraten, und das sind sie
für parabolische und nichtparabolische Täler, eine maximale Energie
vorausgesetzt werden muß, die von den Teilchen zu keinem Zeitpunkt der
Simulation überschritten werden darf.
Wählt man für diese Energie einen
zu großen Wert, so steigt der Selbststreuanteil.
Wird sie zu klein gewählt, kann die
physikalische Streurate im darüberliegenden Energiebereich
nicht mehr exakt reproduziert werden.
den
Nachteil, daß im Fall monoton steigender Streuraten, und das sind sie
für parabolische und nichtparabolische Täler, eine maximale Energie
vorausgesetzt werden muß, die von den Teilchen zu keinem Zeitpunkt der
Simulation überschritten werden darf.
Wählt man für diese Energie einen
zu großen Wert, so steigt der Selbststreuanteil.
Wird sie zu klein gewählt, kann die
physikalische Streurate im darüberliegenden Energiebereich
nicht mehr exakt reproduziert werden.




Next: 5.2 Ein verbesserter Selbststreualgorithmus
Up: 5 Numerische Aspekte
Previous: 5 Numerische Aspekte
Martin Stiftinger
Wed Oct 12 11:59:33 MET 1994
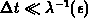 genügt, so kann diese Integralgleichung
direkt
verwendet werden, indem man die Integration numerisch ausführt.
Dies ist vor allen in jenen Fällen sinnvoll, in denen
genügt, so kann diese Integralgleichung
direkt
verwendet werden, indem man die Integration numerisch ausführt.
Dies ist vor allen in jenen Fällen sinnvoll, in denen 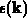 und
und
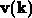 numerisch gegeben sind und die Bewegungsgleichungen zeitdiskret
gelöst werden müssen.
numerisch gegeben sind und die Bewegungsgleichungen zeitdiskret
gelöst werden müssen.




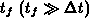 direkt berechnet werden, ohne Zustände an den
dazwischenliegenden Zeitpunkten
direkt berechnet werden, ohne Zustände an den
dazwischenliegenden Zeitpunkten 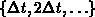 berechnen
zu müssen.
berechnen
zu müssen.
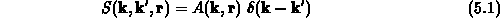
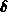 -Funktion bewirkt, daß bei dieser Streuung
keine Änderung des Zustandes
-Funktion bewirkt, daß bei dieser Streuung
keine Änderung des Zustandes 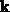 erfolgt, weshalb man auch von
Selbststreuung spricht
erfolgt, weshalb man auch von
Selbststreuung spricht 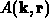 verwendet man nun dazu,
die totale Streurate zu einer Konstanten
verwendet man nun dazu,
die totale Streurate zu einer Konstanten 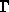 zu machen.
Damit wird der Integrand in Gleichung
zu machen.
Damit wird der Integrand in Gleichung 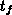 kann einfach bestimmt werden durch
kann einfach bestimmt werden durch
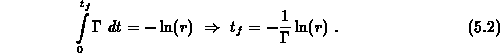
 .
.
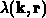 für alle in der Simulation möglichen
für alle in der Simulation möglichen
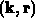 sein. Befindet sich etwa das Elektron in einem Energiebereich,
wo die Streurate klein ist, so werden nach Gleichung
sein. Befindet sich etwa das Elektron in einem Energiebereich,
wo die Streurate klein ist, so werden nach Gleichung 
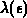 zu
Selbststreurate
zu
Selbststreurate 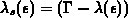 schematisch dargestellt.
Der hohe
Selbststreuanteil bei niedrigen Energien kann durch einen Übergang auf eine
stückweise konstante Begrenzungsfunktion reduziert werden
(Abbildung
schematisch dargestellt.
Der hohe
Selbststreuanteil bei niedrigen Energien kann durch einen Übergang auf eine
stückweise konstante Begrenzungsfunktion reduziert werden
(Abbildung 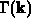 -Abhängigkeit existiert.
-Abhängigkeit existiert.
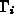 ortsabhängig gewählt. Die Mittelwerte können
mit der ,,before scattering``-Methode
gebildet werden. Durch Verwendung kleiner Energieintervalle kann die
Selbststreurate wirkungsvoll reduziert werden, jedoch erhöht sich der
Rechenaufwand. Die Anzahl der Parameter zur Beschreibung der orts- und
energieabhängigen Treppenfunktion dürfte relativ hoch sein.
Dieses Verfahren hat ebenso wie das mit durchgehend konstantem
ortsabhängig gewählt. Die Mittelwerte können
mit der ,,before scattering``-Methode
gebildet werden. Durch Verwendung kleiner Energieintervalle kann die
Selbststreurate wirkungsvoll reduziert werden, jedoch erhöht sich der
Rechenaufwand. Die Anzahl der Parameter zur Beschreibung der orts- und
energieabhängigen Treppenfunktion dürfte relativ hoch sein.
Dieses Verfahren hat ebenso wie das mit durchgehend konstantem