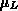 und der Sättigungsgeschwindigkeit
und der Sättigungsgeschwindigkeit 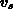 modelliert [94],
modelliert [94],




Legt man den Übergang zwischen dem erweiterten Drift-Diffusionsmodell und dem Monte-Carlo-Modell in einen Bereich des Bauelementes, in dem das Feld hoch, aber möglichst uniform ist, so muß gewährleistet sein, daß die Trägertemperatur aus dem lokalen Modell mit jener aus dem Monte-Carlo-Modell übereinstimmt.
Die Energierelaxationszeit, die nach der Ableitung von Hänsch als konstant
angenommen wird, wird in MINIMOS in Abhängigkeit von der Gitterbeweglichkeit
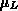 und der Sättigungsgeschwindigkeit
und der Sättigungsgeschwindigkeit 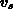 modelliert [94],
modelliert [94],
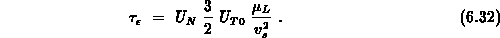
Der Parameter 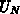 kann frei zwischen 0 und 1 gewählt werden und besitzt die
Voreinstellung von 0.8. Für den im folgenden gezeigten Vergleich mit
Monte-Carlo-Rechnungen hat sich ein Wert von
kann frei zwischen 0 und 1 gewählt werden und besitzt die
Voreinstellung von 0.8. Für den im folgenden gezeigten Vergleich mit
Monte-Carlo-Rechnungen hat sich ein Wert von 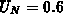 als vorteilhaft erwiesen, womit
die Energierelaxationszeiten bei den betrachteten Gittertemperaturen die
Werte
als vorteilhaft erwiesen, womit
die Energierelaxationszeiten bei den betrachteten Gittertemperaturen die
Werte
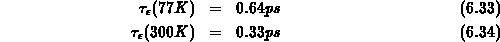
annehmen. Die mittlere Energie ergibt sich aus dem lokalen Temperaturmodell (Gleichung 6.26) gemäß
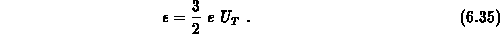
In Abbildung 6.3 ist nun ein Vergleich dieses lokalen Energiemodelles (strichpunktiert) mit dem Monte-Carlo-Modell (durchgezogene Linie) dargestellt . Ähnlich wie beim Vergleich der Driftgeschwindigkeiten in Abbildung 6.1 ist auch hier bei 300K die Übereinstimmung gut, während sie bei 77K schlecht ist. Um eine Erklärung für die Abweichung bei 77K zu finden, soll die Energierelaxationszeit, die im lokalen Trägertemperaturmodell (Gleichung 6.26) eine zentrale Rolle spielt, mit jener aus dem Monte-Carlo-Modell verglichen werden.
Der allgemeine Relaxationszeitansatz Gleichung 4.5 nimmt
im Fall der mittleren Energie 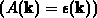 die Form
die Form
an. Diese Gleichung soll nun nicht als Annäherung der mittleren
Energieabgaberate auf der linken Seite durch die einfachere rechte Seite dienen,
sondern vielmehr als Bestimmungsgleichung für die Energierelaxationszeit 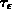 .
.
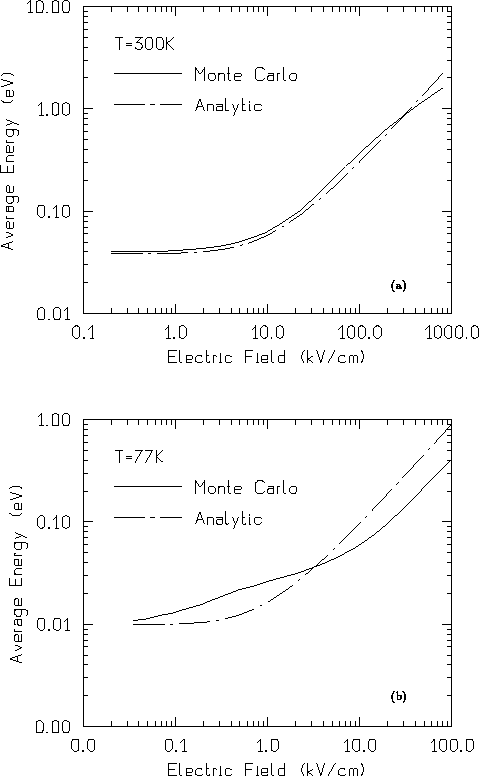
Abbildung: Mittlere Energie der Elektronen als Funktion des elektrischen Feldes
aus dem Monte-Carlo-Modell und aus der lokalen Relaxationszeitnäherung.
Die Coulombstreuung und die akustische Innertalstreuung sind elastisch,
sodaß sie im Streuintegral in Gleichung 6.36
wegen 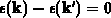 keinen Beitrag
liefern. Einzig die Zwischentalstreuung ist inelastisch, wobei die
Energiedifferenz der Phononenenergie
keinen Beitrag
liefern. Einzig die Zwischentalstreuung ist inelastisch, wobei die
Energiedifferenz der Phononenenergie
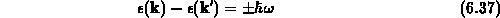
entspricht, die im verwendeten Modell konstant ist.
Werden in einem Modell 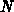 verschiedenen Phononenstreumechanismen
berücksichtigt, so erhält man aus Gleichung 6.36 nach kurzer
Zwischenrechnung
verschiedenen Phononenstreumechanismen
berücksichtigt, so erhält man aus Gleichung 6.36 nach kurzer
Zwischenrechnung
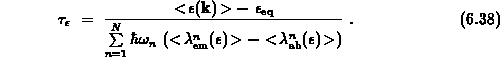
Darin bedeutet 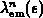 die totale Streurate
bei Emission des n-ten Phonons (Gleichung 3.49), und
die totale Streurate
bei Emission des n-ten Phonons (Gleichung 3.49), und
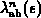 die totale Streurate bei Phononenabsorption
(Gleichung 3.47).
die totale Streurate bei Phononenabsorption
(Gleichung 3.47).
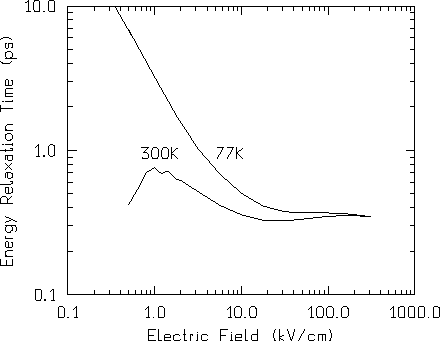
Abbildung: Energierelaxationszeit als Funktion der Feldstärke aus dem Monte-Carlo-Modell.
Die so definierte Energierelaxationszeit kann als Funktion der Feldstärke mit Hilfe der Monte-Carlo-Methode ausgewertet werden. Abbildung 6.4 zeigt einen Vergleich der Ergebnisse bei einer Gittertemperatur von 77K und 300K.
Man erkennt, daß die Annahme einer konstanten Energierelaxationszeit im lokalen Trägertemperaturmodell einer kritischen Betrachtung bedarf, da insbesondere bei 77K eine größere Variation feststellbar ist.
Um die Situation genauer analysieren zu können, muß auch die Beweglichkeit miteinbezogen werden. Die Beweglichkeit wird, wie schon erwähnt wurde, aus einer lokalen Lösung der Momentengleichungen gewonnen. Diese können nach Weglassen der Ortsableitungen angeschrieben werden als [33] [34]
Darin bedeutet 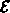 die Energiedichte der Elektronen, die mit der
Temperaturspannung in dem
Zusammenhang
die Energiedichte der Elektronen, die mit der
Temperaturspannung in dem
Zusammenhang
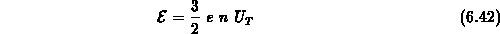
steht. Setzt man in die Impulsrelaxationszeit (Gleichung 6.23) den Energiestrom aus der dritten Momentengleichung 6.41 ein, so sieht man, daß die Beweglichkeit eine direkte Funktion der mittleren Energie ist,
wobei in 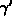 verschiedene Konstanten zusammengefaßt sind.
verschiedene Konstanten zusammengefaßt sind.
Dieses Ergebnis bestätigt in sehr anschaulicher Weise die Erwartung, daß das
nichtlineare Transportverhalten, also ein Abweichen von der Ohmschen Beweglichkeit
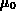 , durch die Erhöhung der Trägerenergie bei hohen Feldern
verursacht wird. Diese Energieerhöhung resultiert nach Gleichung 6.40 aus
der Joulschen Wärme
, durch die Erhöhung der Trägerenergie bei hohen Feldern
verursacht wird. Diese Energieerhöhung resultiert nach Gleichung 6.40 aus
der Joulschen Wärme 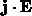 , in die über die Stromdichte
, in die über die Stromdichte  wieder
die Beweglichkeit eingeht. Faßt man also die Gleichungen 6.39 und
6.40 zusammen, ergibt sich für die in der Beweglichkeit benötigten
Energiedifferenz der Ausdruck
wieder
die Beweglichkeit eingeht. Faßt man also die Gleichungen 6.39 und
6.40 zusammen, ergibt sich für die in der Beweglichkeit benötigten
Energiedifferenz der Ausdruck
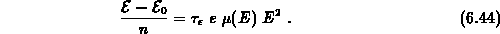
Dies ist der Grund, warum im vorliegenden Modell die Beweglichkeit und die Trägertemperatur nur gemeinsam analysiert werden können.
Nach Abbildung 6.4 kann bei 300K, vor allem bei höheren Feldstärken, die Energierelaxationszeit noch am ehesten mit einer Konstanten angenähert werden. Diese Näherung wird zwar bei kleineren Feldstärken etwas schlechter, jedoch tritt in diesem Bereich keine nennenswerte Energieerhöhung auf. Abbildung 6.3 a bestätigt, daß bei 300K mit einer konstanten Energierelaxationszeit die Trägerenergie mit ausreichender Genauigkeit vorausgesagt werden kann. Damit wird aber nach Gleichung 6.43 auch die Beweglichkeit genau beschrieben, in Übereinstimmung mit Abbildung 6.1.
Bei 77K hingegen ist die Energierelaxationszeit keineswegs konstant, sondern ändert sich um
mehr als eine Größenordnung (Abbildung 6.4). Dementsprechend stimmen
die Werte der Trägerenergie und auch die Form des Verlaufes bis über
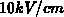 nicht mit dem Monte-Carlo-Ergebnis überein (Abbildung 6.3 b).
Die Abweichung der Driftgeschwindigkeit in Abbildung 6.1, die bis zu einer
Feldstärke von
nicht mit dem Monte-Carlo-Ergebnis überein (Abbildung 6.3 b).
Die Abweichung der Driftgeschwindigkeit in Abbildung 6.1, die bis zu einer
Feldstärke von 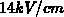 dargestellt ist, kann somit auf die Trägerenergie,
die in diesem Feldstärkenbereich nicht stimmt, zurückgeführt werden.
dargestellt ist, kann somit auf die Trägerenergie,
die in diesem Feldstärkenbereich nicht stimmt, zurückgeführt werden.



