


Next: 6.2.2 Eigenschaften der Methode
Up: 6.2 Implementierte Fehlerabschätzung
Previous: 6.2 Implementierte Fehlerabschätzung
Sei
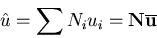 |
(6.4) |
die Näherungslösung des betrachteten Problems mit der Ordnung p, wobei Ni die
Formfunktionen und ui die zugehörigen Beiwerte darstellen. Weiters sei
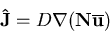 |
(6.5) |
der Partikelfluß anhand der Näherung mit der Ordnung (p-1).
Dann setzen wir für diesen Fluß
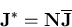 |
(6.6) |
mit der Ordnung p an, welcher 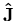 approximiert und mittels gewichteter Residuen
entsprechend
approximiert und mittels gewichteter Residuen
entsprechend
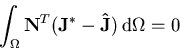 |
(6.7) |
ermittelt wird, woraus man
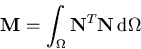 |
(6.8) |
als Systemmatrix erhält. Offensichtlich muß hier also ein Gleichungssystem mit der n-fachen
Ordnung des Originalsystems gelöst werden, wobei n der Anzahl der Raumdimensionen des
Problems entspricht.
Je nach Grad der Nichtlinearität des zugrundeliegenden Problemes sind in der Regel innerhalb
der nichtlinearen Iterationsschleife mehrere Iterationen bis zur Konvergenz nötig. Aufgrund
des sehr lokalen Charakters von Gl. 6.8 kann die Lösung näherungsweise mittels
Gauß-Seidel-Iterationen effizient erfolgen, wenn man diese gemeinsam mit jeder Newton-Iteration
des zugrundeliegenden Problemes durchführt. Die Lösung des aus Gl. 6.8
resultierenden Systems kann also entsprechend
![\begin{displaymath}
\mathbf {J^*}_{n+1} = \mathbf {J^*}_n - \mathbf {C}^{-1} [ \mathbf {M} (\mathbf {J^*}_n - \mathbf {\hat J})]
\end{displaymath}](img257.gif) |
(6.9) |
ohne großen Rechenaufwand erfolgen, worin 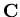 die diagonalisierte Form der Matrix
die diagonalisierte Form der Matrix
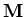 darstellt. Die meisten der für dieses Iterationsverfahren
notwendigen Terme sind ohnehin für die Diskretisierung der Differentialgleichung selbst nötig,
sodaß der Mehraufwand sehr gering bleibt.
darstellt. Die meisten der für dieses Iterationsverfahren
notwendigen Terme sind ohnehin für die Diskretisierung der Differentialgleichung selbst nötig,
sodaß der Mehraufwand sehr gering bleibt.
Derart erhält man mit geringem Aufwand eine genauere Approximierung des Gradienten, welche
formal einer Approximierung der höheren Ableitungen der Näherungslösung
entspricht [Zhu90] [Ain89]. Abb. 6.1 veranschaulicht die verbesserte Näherung
durch eine stückweise lineare Approximierung einer stückweise konstanten Näherung.
Auf der Basis dieses genaueren Gradienten des Funktionsverlaufes kann nun wiederum die
Differentialgleichung diskretisiert werden, indem 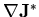 berechnet wird. Die
Differenz
berechnet wird. Die
Differenz 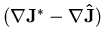 kann dann als Maß für den Fehler aufgrund
der Vernachlässigung des Restgliedes in der Diskretisierung verwendet werden.
kann dann als Maß für den Fehler aufgrund
der Vernachlässigung des Restgliedes in der Diskretisierung verwendet werden.
Zur Überprüfung dieser Annahme wählen wir den Spezialfall eines eindimensionalen
äquidistanten Gitters und betrachten einen Ausschnitt von fünf nebeneinander liegenden
Stützstellen rund um die Stelle x0. In erster Näherung kann in Gl. 6.9 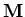 gegen
gegen  ersetzt werden, wodurch man eine einfache Mittelwertbildung der Gradienten
erhält. Unter diesen Voraussetzungen errechnet sich die auf der Basis des stückweise linearen
Gradienten ermittelte, zweite Ortsableitung der Funktion gleich wie die, auf der Basis des
stückweise konstanten Gradienten ermittelte zweite Ableitung, nur mit dem Unterschied, daß die
doppelte Gitterweite eingesetzt wird. Der Einfluß der zweiten und vierten Stützstelle
verschwindet:
ersetzt werden, wodurch man eine einfache Mittelwertbildung der Gradienten
erhält. Unter diesen Voraussetzungen errechnet sich die auf der Basis des stückweise linearen
Gradienten ermittelte, zweite Ortsableitung der Funktion gleich wie die, auf der Basis des
stückweise konstanten Gradienten ermittelte zweite Ableitung, nur mit dem Unterschied, daß die
doppelte Gitterweite eingesetzt wird. Der Einfluß der zweiten und vierten Stützstelle
verschwindet:
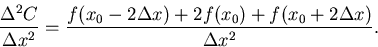 |
(6.10) |
Anstatt einer genaueren Abschätzung erhält man also ungenauere Werte für die zweite
Ableitung. Diese Eigenschaft bleibt auch erhalten, wenn man anstatt der vereinfachenden
Mittelwertbildung Gl. 6.7 löst. Durch den globaleren Charakter der
Fehlerabschätzung ist der Diskretisierungsfehler der so ermittelten Divergenz zwar größer
als der Fehler der eigentlichen Diskretisierung, jedoch gilt mit guter Näherung
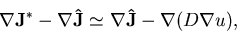 |
(6.11) |
wobei die rechte Seite dem Diskretisierungsfehler der eigentlichen Diskretisierung entspricht,
wenn u für die exakte Lösung steht.



Next: 6.2.2 Eigenschaften der Methode
Up: 6.2 Implementierte Fehlerabschätzung
Previous: 6.2 Implementierte Fehlerabschätzung
Ernst Leitner
1997-12-30
![]() berechnet wird. Die
Differenz
berechnet wird. Die
Differenz ![]() kann dann als Maß für den Fehler aufgrund
der Vernachlässigung des Restgliedes in der Diskretisierung verwendet werden.
kann dann als Maß für den Fehler aufgrund
der Vernachlässigung des Restgliedes in der Diskretisierung verwendet werden.![]() gegen
gegen ![]() ersetzt werden, wodurch man eine einfache Mittelwertbildung der Gradienten
erhält. Unter diesen Voraussetzungen errechnet sich die auf der Basis des stückweise linearen
Gradienten ermittelte, zweite Ortsableitung der Funktion gleich wie die, auf der Basis des
stückweise konstanten Gradienten ermittelte zweite Ableitung, nur mit dem Unterschied, daß die
doppelte Gitterweite eingesetzt wird. Der Einfluß der zweiten und vierten Stützstelle
verschwindet:
ersetzt werden, wodurch man eine einfache Mittelwertbildung der Gradienten
erhält. Unter diesen Voraussetzungen errechnet sich die auf der Basis des stückweise linearen
Gradienten ermittelte, zweite Ortsableitung der Funktion gleich wie die, auf der Basis des
stückweise konstanten Gradienten ermittelte zweite Ableitung, nur mit dem Unterschied, daß die
doppelte Gitterweite eingesetzt wird. Der Einfluß der zweiten und vierten Stützstelle
verschwindet: