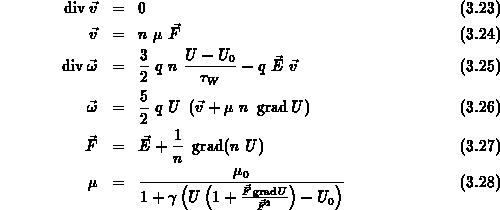3.1.1 Boltzmanngleichung und Momentenmethode




Next: 3.1.2 Das lokale ``Hot
Up: 3.1 Die Halbleitergleichungen
Previous: 3.1 Die Halbleitergleichungen
Die Poissongleichung und die Kontinuitätsgleichungen für Elektronen und
Löcher lassen sich im Rahmen der makroskopischen Elektrodynamik aus der
dritten und der ersten Maxwellgleichung herleiten (vgl. [76]
Kap. 1). Diese drei Gleichungen sind auch bei einer allgemeineren
Betrachtung des Ladungsträgertransports, die über die
Drift-Diffusionsnäherung hinausgeht, gültig.
Die folgende Herleitung der Trägertransportgleichungen und der funktionalen
Form der zugehörigen Parameter (Beweglichkeit 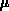 und Temperaturspannung
und Temperaturspannung
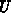 ) folgt im wesentlichen der von Hänsch [25] vorgeschlagenen
Methode. Eine detailliertere Diskussion dieser Ableitung findet man in
[28] und [43]. Die Trägertransportgleichung wird im
folgenden für Elektronen abgeleitet und gilt mit trivialen Änderungen auch
für Löcher.
) folgt im wesentlichen der von Hänsch [25] vorgeschlagenen
Methode. Eine detailliertere Diskussion dieser Ableitung findet man in
[28] und [43]. Die Trägertransportgleichung wird im
folgenden für Elektronen abgeleitet und gilt mit trivialen Änderungen auch
für Löcher.
Um einen Zusammenhang zwischen der Stromdichte, dem elektrostatischen Potential 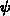 und der Ladungsträgerdichte
und der Ladungsträgerdichte
 zu erhalten, betrachten wir nun die Verteilung der Ladungsträger
im Phasenraum, der aus drei Ortskoordinaten
zu erhalten, betrachten wir nun die Verteilung der Ladungsträger
im Phasenraum, der aus drei Ortskoordinaten 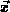 , drei Impulskoordinaten
, drei Impulskoordinaten
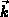 und der Zeit
und der Zeit 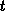 gebildet wird. Zur Beschreibung eines Kollektivs von
Ladungsträgern dient die Verteilungsfunktion
gebildet wird. Zur Beschreibung eines Kollektivs von
Ladungsträgern dient die Verteilungsfunktion 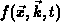 , die die
Wahrscheinlichkeit der Besetzung eines Zustands mit bestimmtem Ort
, die die
Wahrscheinlichkeit der Besetzung eines Zustands mit bestimmtem Ort 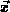 und
bestimmtem Impuls
und
bestimmtem Impuls 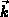 zur Zeit
zur Zeit 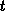 im Phasenraum angibt. Die totale
Ableitung der Verteilungsfunktion
im Phasenraum angibt. Die totale
Ableitung der Verteilungsfunktion 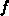 nach der Zeit ergibt
die Boltzmanngleichung (3.6). Diese
beschreibt die ``örtliche'' (Ort
nach der Zeit ergibt
die Boltzmanngleichung (3.6). Diese
beschreibt die ``örtliche'' (Ort 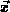 und Impuls
und Impuls 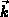 ) und zeitliche
Änderung der Verteilungsfunktion in Abhängigkeit von äußeren und inneren
Kräften. Äußere Kräfte werden in unserem Fall nur durch das elektrische
Feld
) und zeitliche
Änderung der Verteilungsfunktion in Abhängigkeit von äußeren und inneren
Kräften. Äußere Kräfte werden in unserem Fall nur durch das elektrische
Feld 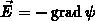 hervorgerufen. Die inneren Kräfte umfassen
sämtliche Streuprozesse und Interaktionen zwischen den Ladungsträgern
untereinander
und den Ladungsträgern mit dem Kristallgitter. Während die äußere Kraft
in einfacher Weise durch
hervorgerufen. Die inneren Kräfte umfassen
sämtliche Streuprozesse und Interaktionen zwischen den Ladungsträgern
untereinander
und den Ladungsträgern mit dem Kristallgitter. Während die äußere Kraft
in einfacher Weise durch 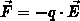 ausgedrückt werden kann,
können die inneren Kräfte nur mehr mit statistischen Mitteln erfaßt werden.
ausgedrückt werden kann,
können die inneren Kräfte nur mehr mit statistischen Mitteln erfaßt werden.
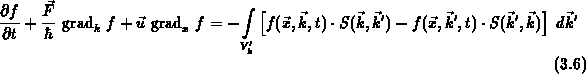
Die Größen 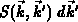 und
und 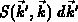 auf der rechten Seite
von Gleichung (3.6) beschreiben die Wahrscheinlichkeit, daß ein
Teilchen aus dem Zustand
auf der rechten Seite
von Gleichung (3.6) beschreiben die Wahrscheinlichkeit, daß ein
Teilchen aus dem Zustand 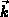 in das Volumselement
in das Volumselement 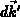 hinein, bzw.
aus dem Volumselement
hinein, bzw.
aus dem Volumselement 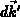 herausgestreut wird. Mit
herausgestreut wird. Mit 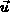 wird die
Gruppengeschwindigkeit
wird die
Gruppengeschwindigkeit 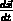 bezeichnet.
bezeichnet.
Um Aussagen über die Verteilungsfunktion zu erhalten, kann
(3.6) selbst gelöst werden.
Dies ist praktisch nur mit mithilfe von Monte-Carlo-Methoden
[35] möglich, wobei die Trajektorien einer großen Zahl von
Teilchen im mikroskopischen Bereich verfolgt und daraus die
makroskopischen Größen berechnet werden. Diese Methode erfordert einen
enormen Aufwand an Computerresourcen und ist daher für den täglichen Einsatz
in der Entwicklung nur in speziellen Fällen geeignet.
Ein anderer Weg besteht darin, nicht die
exakte Form der Verteilungsfunktion 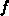 , sondern ihre makroskopischen
Mittelwerte (Momente), die den interessierenden physikalischen
Größen entsprechen, zu berechnen.
, sondern ihre makroskopischen
Mittelwerte (Momente), die den interessierenden physikalischen
Größen entsprechen, zu berechnen.
Die ersten vier Momente der Verteilungsfunktion 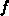 sind die Teilchendichte
sind die Teilchendichte  (3.7), die Teilchenstromdichte
(3.7), die Teilchenstromdichte 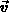 (3.8), die Energiedichte
(3.8), die Energiedichte 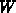 (3.9) und die Energiestromdichte
(3.9) und die Energiestromdichte  (3.10), wobei
(3.10), wobei
 die Bandenergie bezeichnet.
die Bandenergie bezeichnet.
Multipliziert man nun die Boltzmanngleichung (3.6) mit der jeweiligen
Größe und integriert man über den Impulsraum, so erhält man
Erhaltungsgleichungen für die vier Momente. Ohne Information über die genaue
Form der Verteilungsfunktion ist es nicht möglich, die Streuintegrale auf der
rechten Seite von (3.6) direkt auszuwerten. Es ist jedoch möglich, die
Streuintegrale durch einen einfachen Relaxationszeitansatz der Form
zu approximieren. 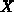 steht hier stellvertretend für die jeweils
zu multiplizierende Größe in (3.7) - (3.10).
Die Relaxationszeit
steht hier stellvertretend für die jeweils
zu multiplizierende Größe in (3.7) - (3.10).
Die Relaxationszeit 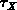 ist im allgemeinen eine von den Momenten
abhängige Größe.
Nach Einführung einer verallgemeinerten Temperaturspannung
ist im allgemeinen eine von den Momenten
abhängige Größe.
Nach Einführung einer verallgemeinerten Temperaturspannung
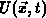 bzw. einer verallgemeinerten Ladungsträgertemperatur
bzw. einer verallgemeinerten Ladungsträgertemperatur
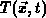 , die der mittleren Teilchenenergie
, die der mittleren Teilchenenergie 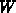 proportional ist,
proportional ist,
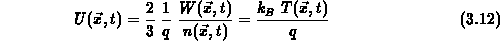
und der Beweglichkeit

erhält man aus der Boltzmanngleichung folgende vier Gleichungen:
- Teilchenerhaltung
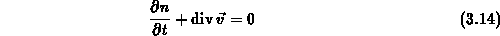
- Teilchenstromdichte
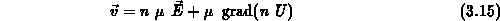
- Energieerhaltung
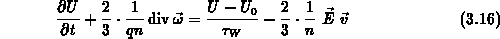
- Energiestromdichte
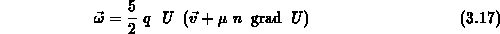
Die Impulsrelaxationszeit 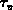 und die Energierelaxationszeit
und die Energierelaxationszeit
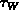 werden
im allgemeinen von den vier Momenten
werden
im allgemeinen von den vier Momenten  ,
, 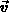 ,
, 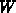 und
und 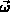 abhängig sein. Da ihre funktionale Form unbekannt ist, bietet sich nun die
Möglichkeit, durch eine geeignete Wahl dieser Abhängigkeiten eine geschlossene
Lösung des Gleichungssystems anzugeben. Durch eine
geeignete Wahl ihrer Werte kann die Lösung an experimentelle Ergebnisse
angepaßt werden.
abhängig sein. Da ihre funktionale Form unbekannt ist, bietet sich nun die
Möglichkeit, durch eine geeignete Wahl dieser Abhängigkeiten eine geschlossene
Lösung des Gleichungssystems anzugeben. Durch eine
geeignete Wahl ihrer Werte kann die Lösung an experimentelle Ergebnisse
angepaßt werden.
Die Impulsrelaxationszeit 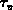 läßt sich nun in der folgenden funktionalen Form
darstellen [28]:
läßt sich nun in der folgenden funktionalen Form
darstellen [28]:
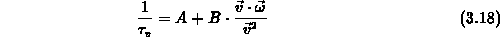
Die Koeffizienten 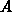 und
und 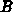 sind dabei nicht mehr von den Momenten
abhängig. Die Energierelaxationszeit
sind dabei nicht mehr von den Momenten
abhängig. Die Energierelaxationszeit 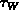 wird ebenfalls von den Momenten
unabhängig angenommen.
wird ebenfalls von den Momenten
unabhängig angenommen.

Nach Einführung der auf die Ladungsträger einwirkenden treibenden Kraft
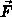 [26]
[26]
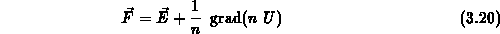
erhält man mithilfe von (3.15) und (3.17) die Abhängigkeit
der Impulsrelaxationszeit von der treibenden Kraft und der mittleren
Teilchenenergie.
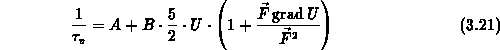
Gleichung (3.21) liefert unter Verwendung von (3.13)
die Abhängigkeit der Beweglichkeit 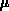 von der treibenden Kraft und
der mittleren Teilchenenergie,
von der treibenden Kraft und
der mittleren Teilchenenergie,
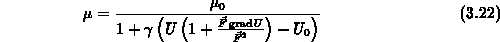
wobei die momentenunabhängigen Koeffizienten 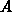 und
und 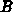 aus (3.21)
durch die ebenfalls momentenunabhängigen Koeffizienten
aus (3.21)
durch die ebenfalls momentenunabhängigen Koeffizienten 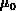 und
und 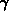 ersetzt wurden, die - wie unten gezeigt wird - leicht aus Grenzwertbetrachtungen
für konstantes elektrisches Feld und homogene Dotierung bestimmt werden
können.
ersetzt wurden, die - wie unten gezeigt wird - leicht aus Grenzwertbetrachtungen
für konstantes elektrisches Feld und homogene Dotierung bestimmt werden
können.
Nach Vernachlässigung der zeitlichen Ableitungen in (3.14) und
(3.16) steht nun
mit (3.23) - (3.28) ein in den ersten vier
Momenten der Boltzmanngleichung geschlossener Gleichungssatz zur Verfügung, aus
den in weiterer Folge Erweiterungen zum klassischen Drift-Diffusionsansatz
(3.4) - (3.5) gewonnen werden können.
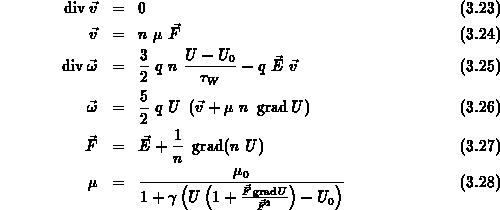
Ziel der weiteren Vorgangsweise ist es, das Gleichungssystem (3.23)
- (3.28) so weit zu reduzieren, daß einerseits die Gleichungsstruktur
des klassischen Drift-Diffusionsansatzes (3.1) - (3.5)
erhalten bleibt, andererseits aber auch die zusätzliche Information, die in
der Energieerhaltungsgleichung
(3.25) und der Energiestromgleichung (3.26) steckt,
mitberücksichtigt wird.




Next: 3.1.2 Das lokale ``Hot
Up: 3.1 Die Halbleitergleichungen
Previous: 3.1 Die Halbleitergleichungen
Martin Stiftinger
Fri Oct 14 19:00:51 MET 1994
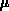 und Temperaturspannung
und Temperaturspannung
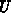 ) folgt im wesentlichen der von Hänsch [25] vorgeschlagenen
Methode. Eine detailliertere Diskussion dieser Ableitung findet man in
[28] und [43]. Die Trägertransportgleichung wird im
folgenden für Elektronen abgeleitet und gilt mit trivialen Änderungen auch
für Löcher.
) folgt im wesentlichen der von Hänsch [25] vorgeschlagenen
Methode. Eine detailliertere Diskussion dieser Ableitung findet man in
[28] und [43]. Die Trägertransportgleichung wird im
folgenden für Elektronen abgeleitet und gilt mit trivialen Änderungen auch
für Löcher.




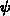 und der Ladungsträgerdichte
und der Ladungsträgerdichte
 zu erhalten, betrachten wir nun die Verteilung der Ladungsträger
im Phasenraum, der aus drei Ortskoordinaten
zu erhalten, betrachten wir nun die Verteilung der Ladungsträger
im Phasenraum, der aus drei Ortskoordinaten 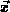 , drei Impulskoordinaten
, drei Impulskoordinaten
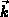 und der Zeit
und der Zeit 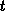 gebildet wird. Zur Beschreibung eines Kollektivs von
Ladungsträgern dient die Verteilungsfunktion
gebildet wird. Zur Beschreibung eines Kollektivs von
Ladungsträgern dient die Verteilungsfunktion 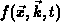 , die die
Wahrscheinlichkeit der Besetzung eines Zustands mit bestimmtem Ort
, die die
Wahrscheinlichkeit der Besetzung eines Zustands mit bestimmtem Ort 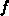 nach der Zeit ergibt
die Boltzmanngleichung (
nach der Zeit ergibt
die Boltzmanngleichung (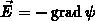 hervorgerufen. Die inneren Kräfte umfassen
sämtliche Streuprozesse und Interaktionen zwischen den Ladungsträgern
untereinander
und den Ladungsträgern mit dem Kristallgitter. Während die äußere Kraft
in einfacher Weise durch
hervorgerufen. Die inneren Kräfte umfassen
sämtliche Streuprozesse und Interaktionen zwischen den Ladungsträgern
untereinander
und den Ladungsträgern mit dem Kristallgitter. Während die äußere Kraft
in einfacher Weise durch 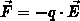 ausgedrückt werden kann,
können die inneren Kräfte nur mehr mit statistischen Mitteln erfaßt werden.
ausgedrückt werden kann,
können die inneren Kräfte nur mehr mit statistischen Mitteln erfaßt werden.
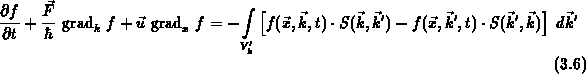
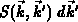 und
und 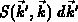 auf der rechten Seite
von Gleichung (
auf der rechten Seite
von Gleichung (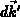 hinein, bzw.
aus dem Volumselement
hinein, bzw.
aus dem Volumselement 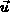 wird die
Gruppengeschwindigkeit
wird die
Gruppengeschwindigkeit 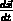 bezeichnet.
bezeichnet.
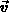 (
(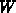 (
(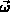 (
(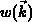 die Bandenergie bezeichnet.
die Bandenergie bezeichnet.
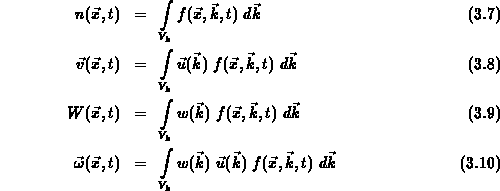
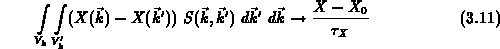
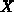 steht hier stellvertretend für die jeweils
zu multiplizierende Größe in (
steht hier stellvertretend für die jeweils
zu multiplizierende Größe in (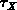 ist im allgemeinen eine von den Momenten
abhängige Größe.
Nach Einführung einer verallgemeinerten Temperaturspannung
ist im allgemeinen eine von den Momenten
abhängige Größe.
Nach Einführung einer verallgemeinerten Temperaturspannung
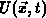 bzw. einer verallgemeinerten Ladungsträgertemperatur
bzw. einer verallgemeinerten Ladungsträgertemperatur
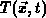 , die der mittleren Teilchenenergie
, die der mittleren Teilchenenergie 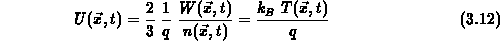

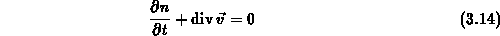
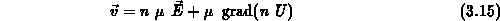
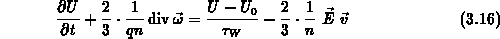
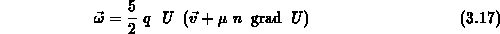
 und die Energierelaxationszeit
und die Energierelaxationszeit
 werden
im allgemeinen von den vier Momenten
werden
im allgemeinen von den vier Momenten 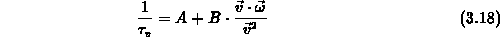
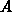 und
und 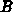 sind dabei nicht mehr von den Momenten
abhängig. Die Energierelaxationszeit
sind dabei nicht mehr von den Momenten
abhängig. Die Energierelaxationszeit 
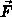
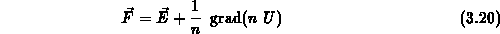
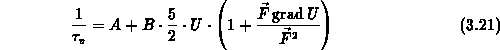
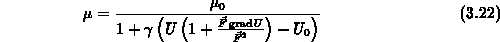
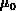 und
und 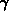 ersetzt wurden, die - wie unten gezeigt wird - leicht aus Grenzwertbetrachtungen
für konstantes elektrisches Feld und homogene Dotierung bestimmt werden
können.
ersetzt wurden, die - wie unten gezeigt wird - leicht aus Grenzwertbetrachtungen
für konstantes elektrisches Feld und homogene Dotierung bestimmt werden
können.